Find the momentof inertia of a uniform square plate of mass m and edge a about one of its diagonals.
Video Solution
Text Solution
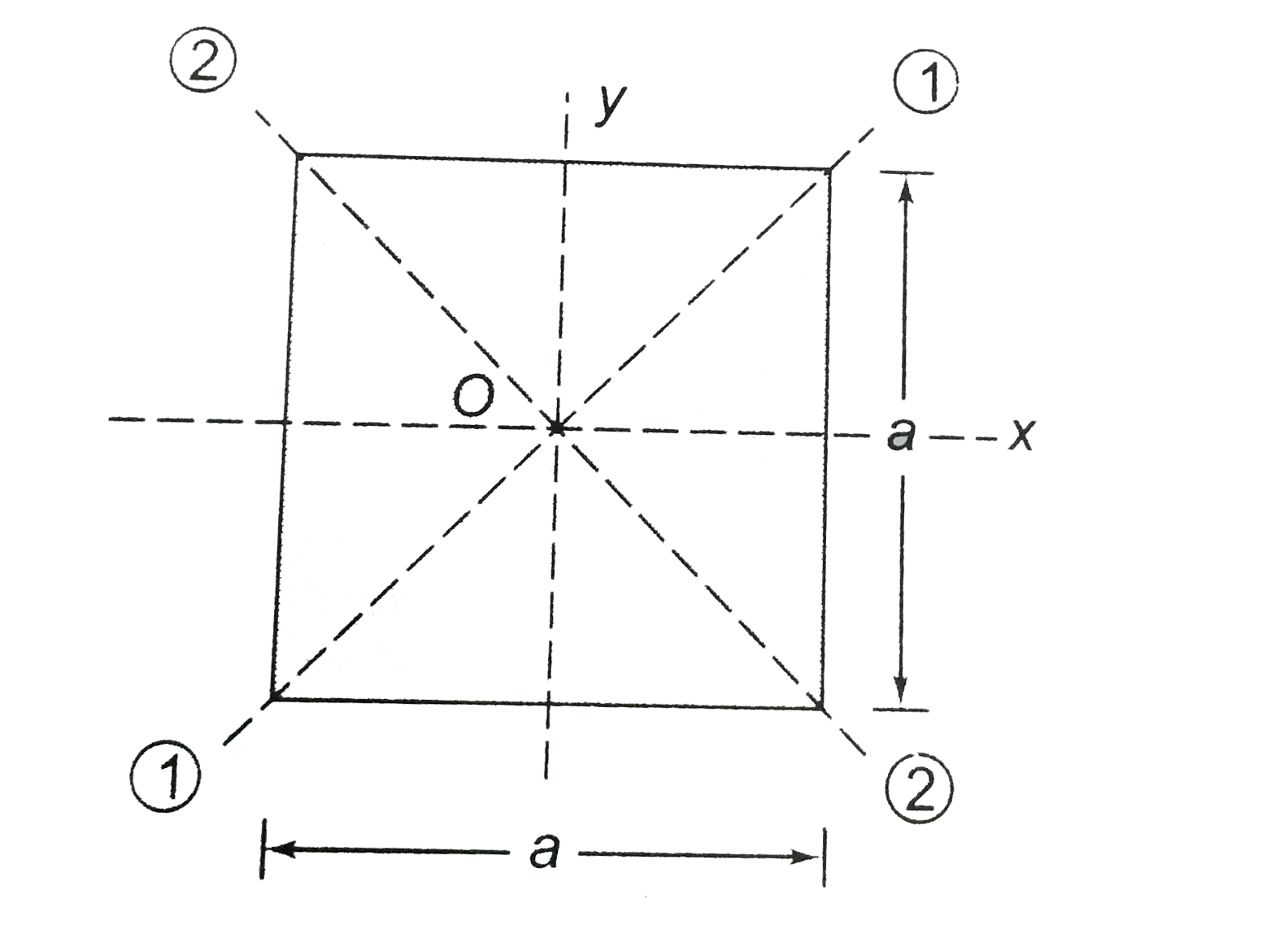
I1−1=?
We know, for square plate
Ix=Iy=ma212
Ix+Iy=Iz (⊥ar axes theorem) (i)
Diagonals of squares are ⊥ar
I1−1+I2−2=Iz (ii)
I1−1+I2−2=Ix+Iy=Iz
By symmetry I1−1=I2−2
I1−1=I2−2=Ix=Iy=ma212
For any axis passing through the center of plate and lying in the x−y plane
I3−3=I4−4=ma212

|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The radius of gyration of a uniform square plate of mass M and side a about its diagonal is
Aa√6Ba2√3Ca2√2Da4 - Question 2 - Select One
The moment of inertia of a cube of mass m and side a about one of its edges is equal to
A23ma2B43ma2C3ma2D83ma2 - Question 3 - Select One
The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.
 View Solution
View SolutionFind the moment of inertia of a uniform rign of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
 View Solution
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
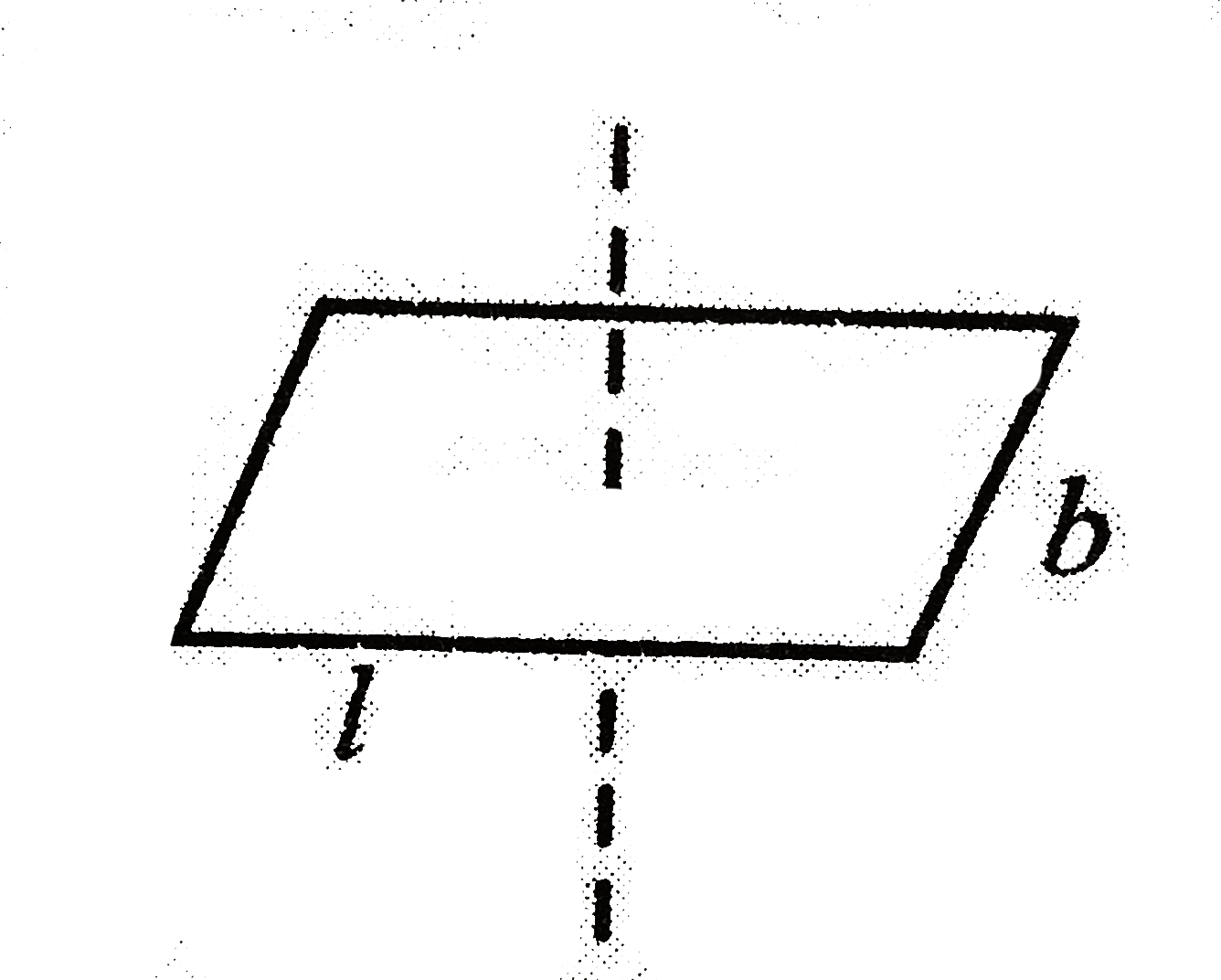 View Solution
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution

