Four identical bars of mass m, length l are connected by pins at A,B,C and D. The bars are attached to four springs of same stiffness as shown. The entire sysetm can move in horizontal plane. In the equilibrium position shown, θ=45∘. if the corners A and C are given small displacements towards each other and released, then time period of vibration is

2π√2M3K
2π√4mK
2π√M4K
2π√MK
The correct Answer is:A
Let the angle turned by the barse be 'θ' after being displaced form equilibrium position. Compression in springs A,C is Δx1=l[cos(45∘−θ)−cos45∘]extension i springs B,D is
Δx2=l[cos45∘−cos(45∘+θ)]
∴ Potential energy
=2[12KΔx21]+2[12KΔx22] ..............(1)

≈Kl2θ2(∵ after simplication)
Kinetic energy =
12I(dθdt), where I=ml212+m(l2tan45∘)2=ml23
∴dE/dt=0⇒ solve for T.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
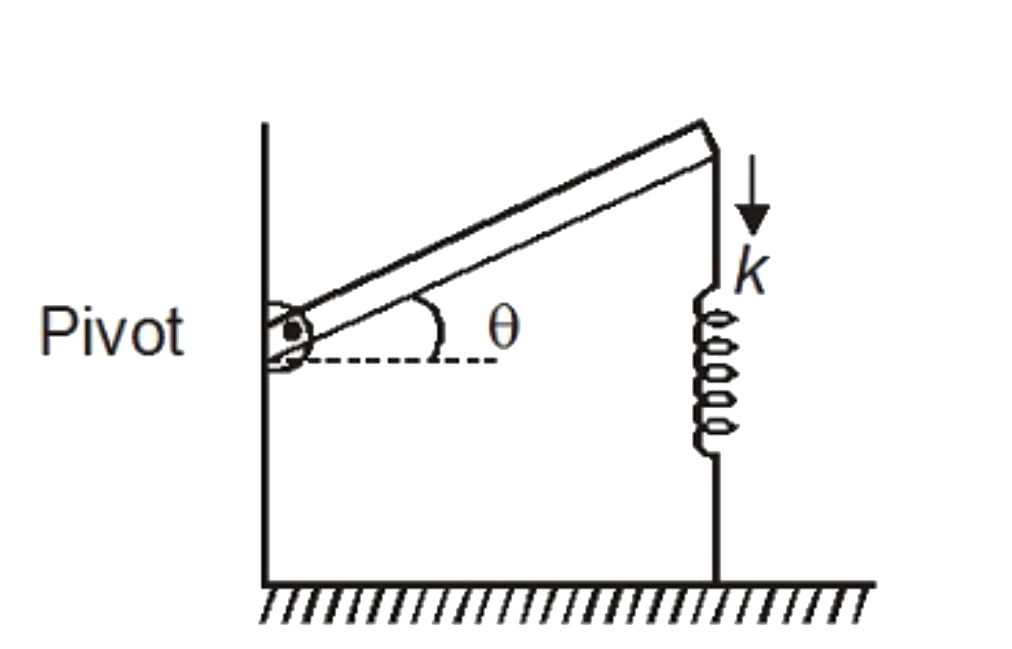
A horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
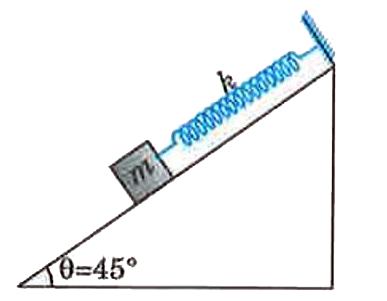
View SolutionA spring of unstretched length 40 cm and spring constant k is attached to a block of mass 1 kg to one of its end. The other end of the spring is fixed on the top of a frictionless inclined plane of inclination θ=45∘ as shown in the figure, so that the spring extends by 3 cm. When the mass is displaced slightly and released the time period of the resulting oscillation is T. Determine the value of 5T close to nearest integer.
View Solution
Knowledge Check
A uniform squre plate of mass m is supported in a horizaontal plane by a vertical pin at B and is attached at A to a spring of constant K. If corner A is given a small displacement and released, determine the period of the resulting motion.
 A2π√2Mb3KB2π√Mb6KCπ√Mb3KDnone of the above
A2π√2Mb3KB2π√Mb6KCπ√Mb3KDnone of the aboveFour identical masses m each are kept at points A, B, C & D shown in figure. Gravitational force on mass at point D (body centre) is -
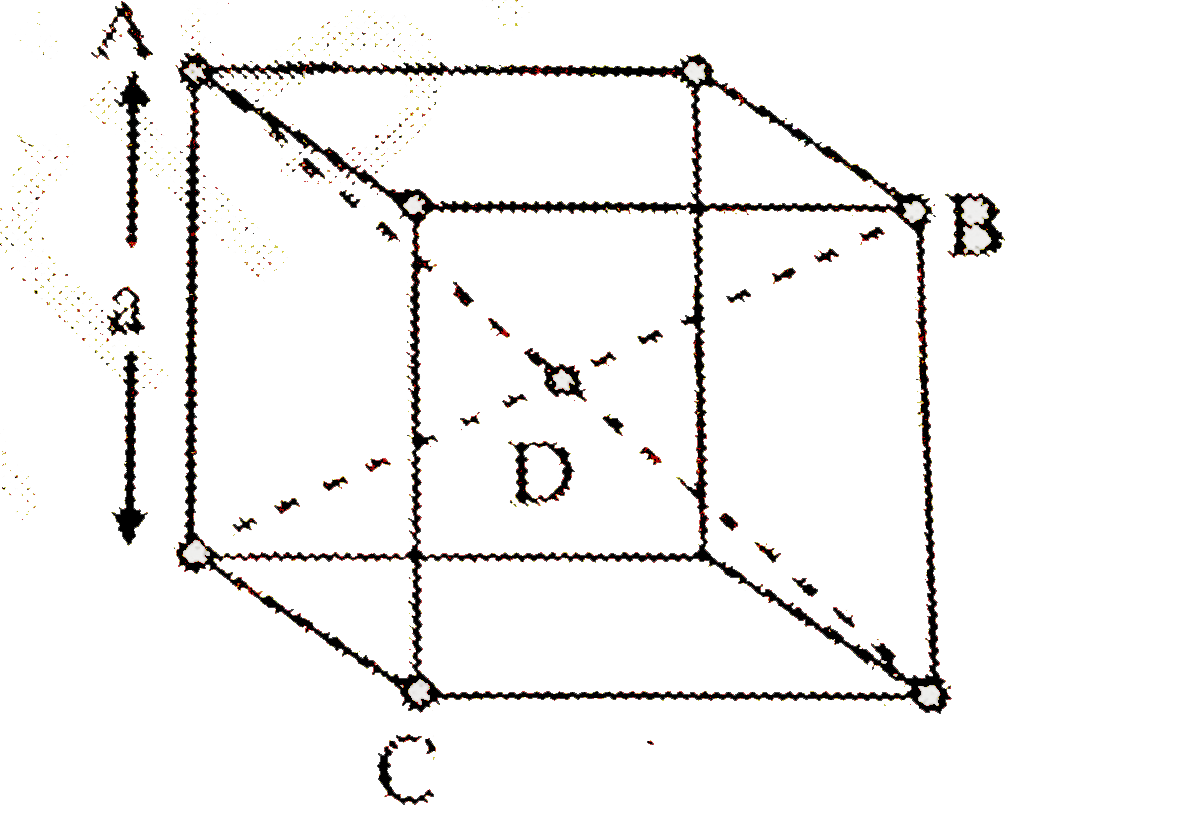 A3Gm2a2B12Gm2a2C4Gm2a2D4Gm23a2
A3Gm2a2B12Gm2a2C4Gm2a2D4Gm23a2Two springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :
 AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
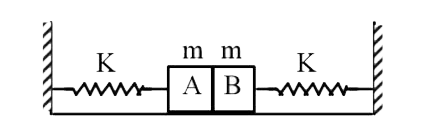
Two blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionA uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-

View Solution
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View SolutionFour rods of equal length L are joined by four pins A,B,C & D as shown in the figure. Rods are free to rotated about pins. Pin A is given velocity v0 and pin C is given 3v0 as shown
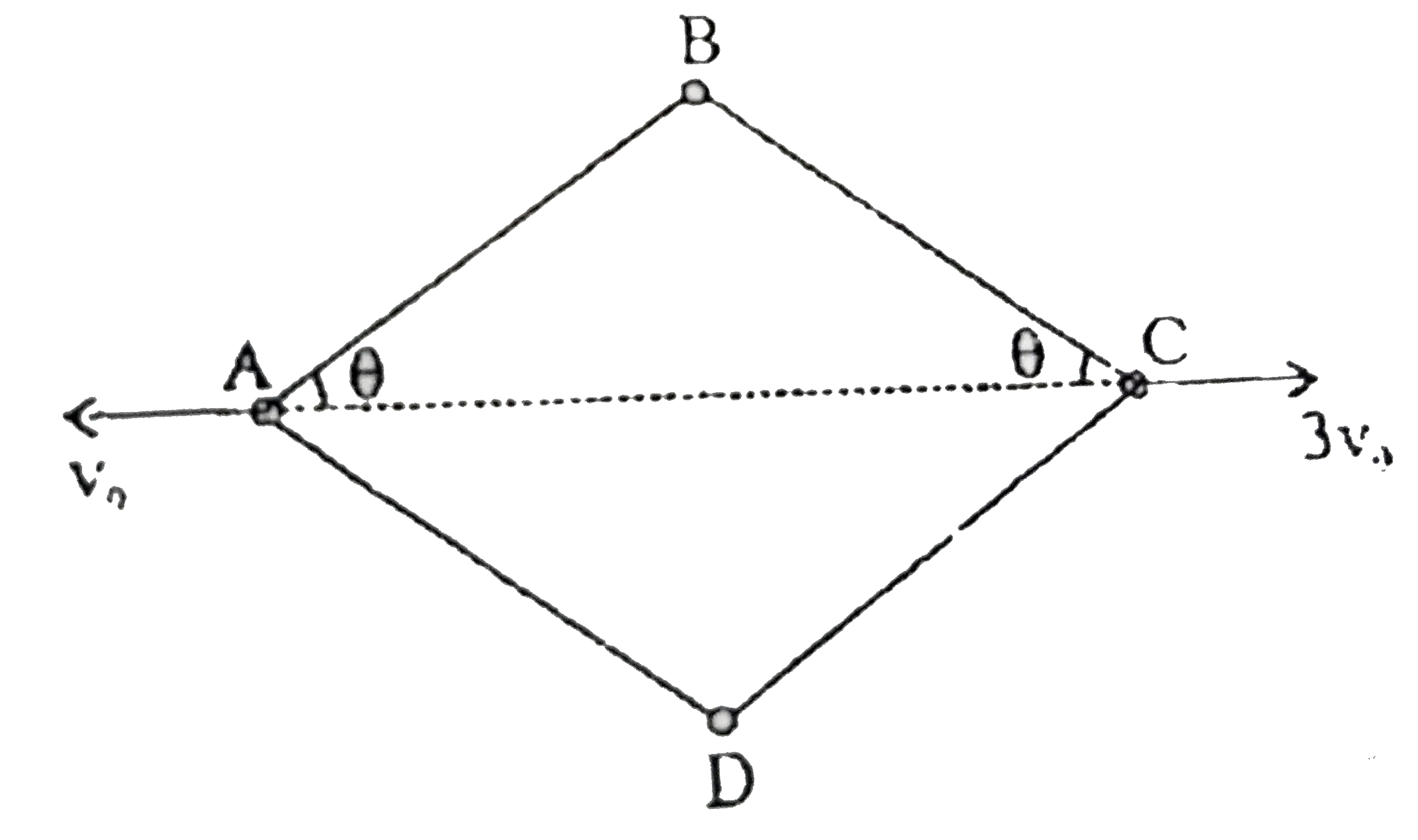
The speed of pin B with respect to pin A is
View Solution
Two springs, each of unstretched length 20 cm but having different spring constant k1=1000Nm and k2=3000Nm are attached to two opposite faces of a small block of mass m=100g kept on a smooth horizontal surface as shown in fig. The outer ends of the two springs are now attached to two pins P1 and P2 whose locations are shown in the figure. as a result of this, the block acquires a new equilibrium position. The block has been displaced by small amount from its equilibrium position and released to perform simple harmonic motion: then
View Solution
