From what minimum height hmust the system be released when spring is unstretches so that after perfectly inelastic collision (e=0) with ground, B may be lifted off the gound: (Spring constant =k)
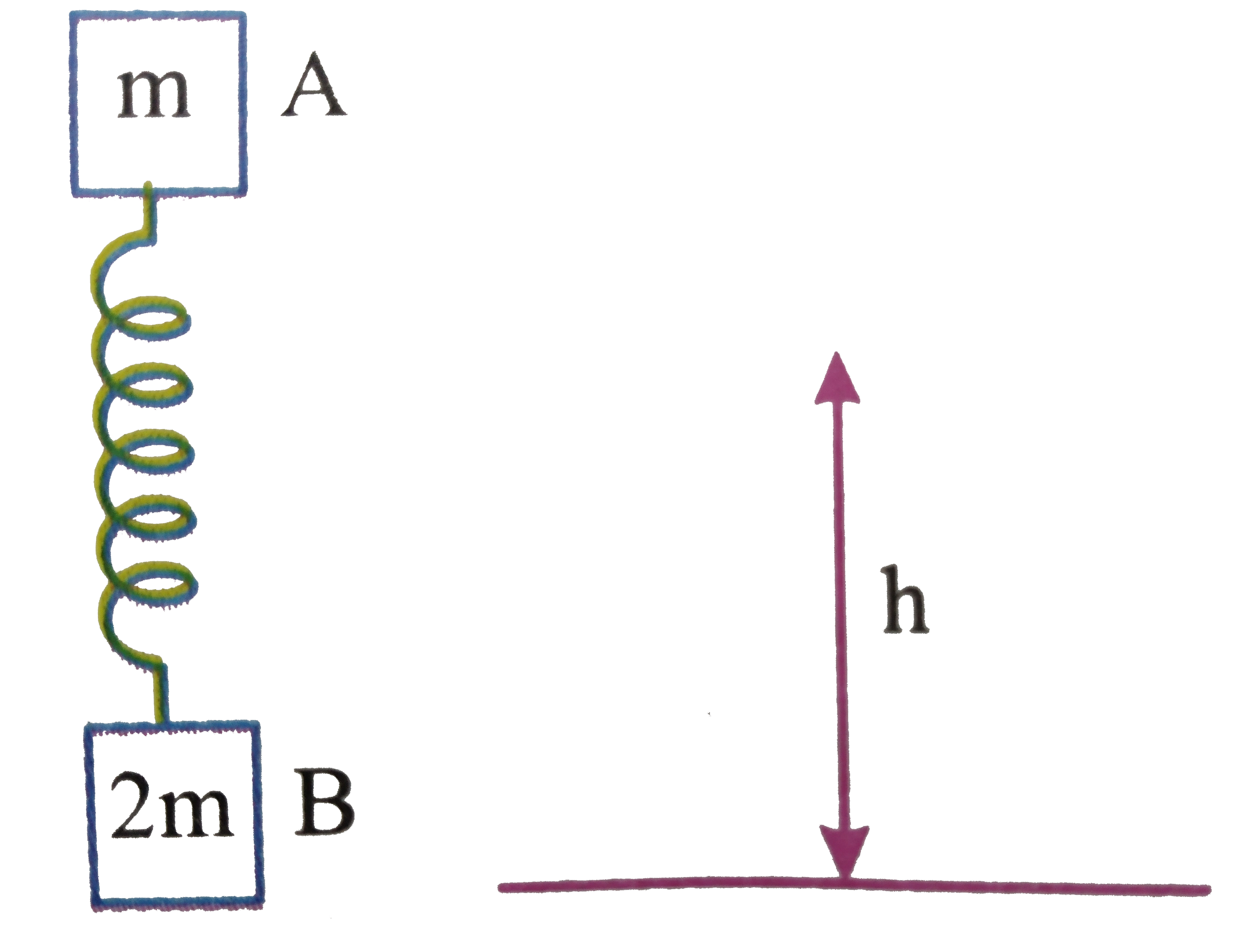
mg/(4k)
4mg/k
mg/(2k)
None of the above
The correct Answer is:B
Just after collision with ground, Applying COE
12mv2+mgx+12kx2=12m(2gh)+0+0
⇒12mv2>0⇒h>4mg/k
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage33videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?View Solutionmass ‘m’ is projected vertically upwards with a speed ‘u’ and at the same instance another particle of mass ‘m’ is released from height ‘h’ vertically above the first particle. The two particles suffer a perfectly inelastic collision, and again reach a maximum height ‘h’ as one combined particle. What is the value of u?
View Solution
Knowledge Check
- Question 1 - Select One
A tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
Ahe6Be2hCe3hDNone of these - Question 2 - Select One
A tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
Ahe6Be2hCe3hDNone of these - Question 3 - Select One
A block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
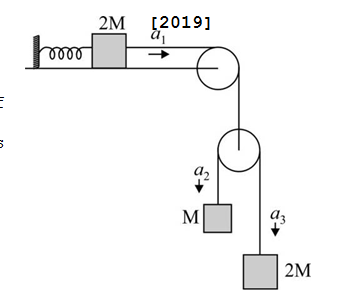 Aa2−a1=a1−a2BAt an extension of x04of the spring, the magnitude of acceleration of the block connected to the spring is 3g10Cx0=4MgkDWhen spring achieves an extension of x02 for the first time, the speed of the block connected to the spring is 3g(M)5K
Aa2−a1=a1−a2BAt an extension of x04of the spring, the magnitude of acceleration of the block connected to the spring is 3g10Cx0=4MgkDWhen spring achieves an extension of x02 for the first time, the speed of the block connected to the spring is 3g(M)5K
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
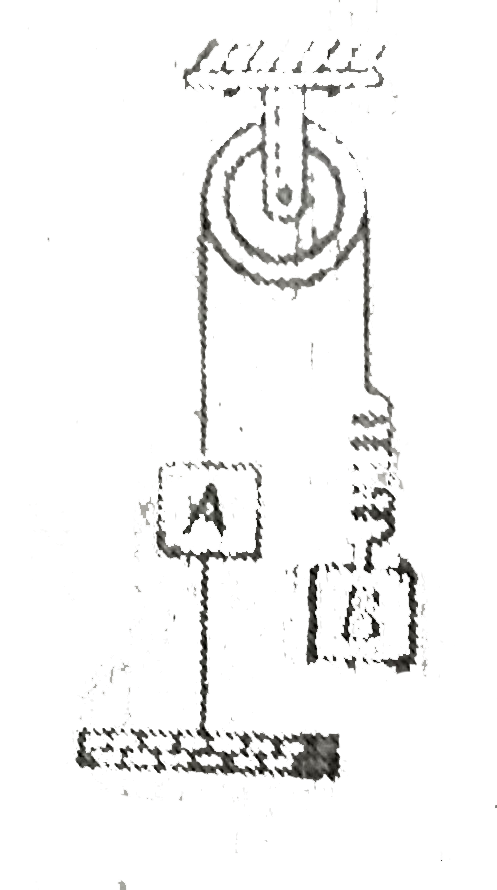 View Solution
View SolutionIn an arrangement shown , bob A on the left is pulled aside . It is then released and allowed to collide with other bob B which is at rest . A perfectly inelastic collision occurs and the system rises to a height h/4 . The ratio of the masses of the bobs is
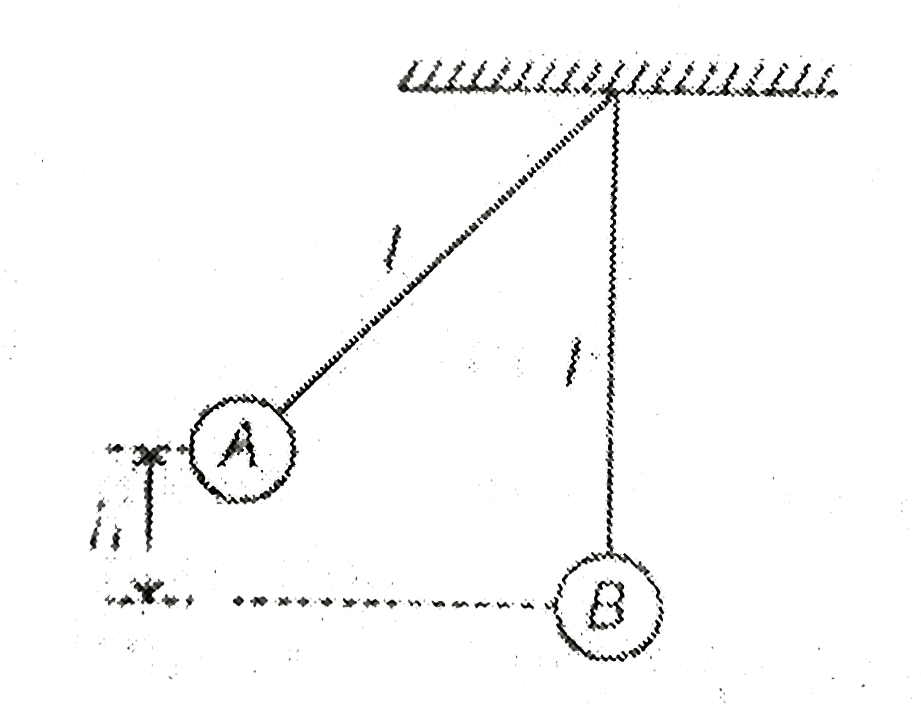 View Solution
View Solution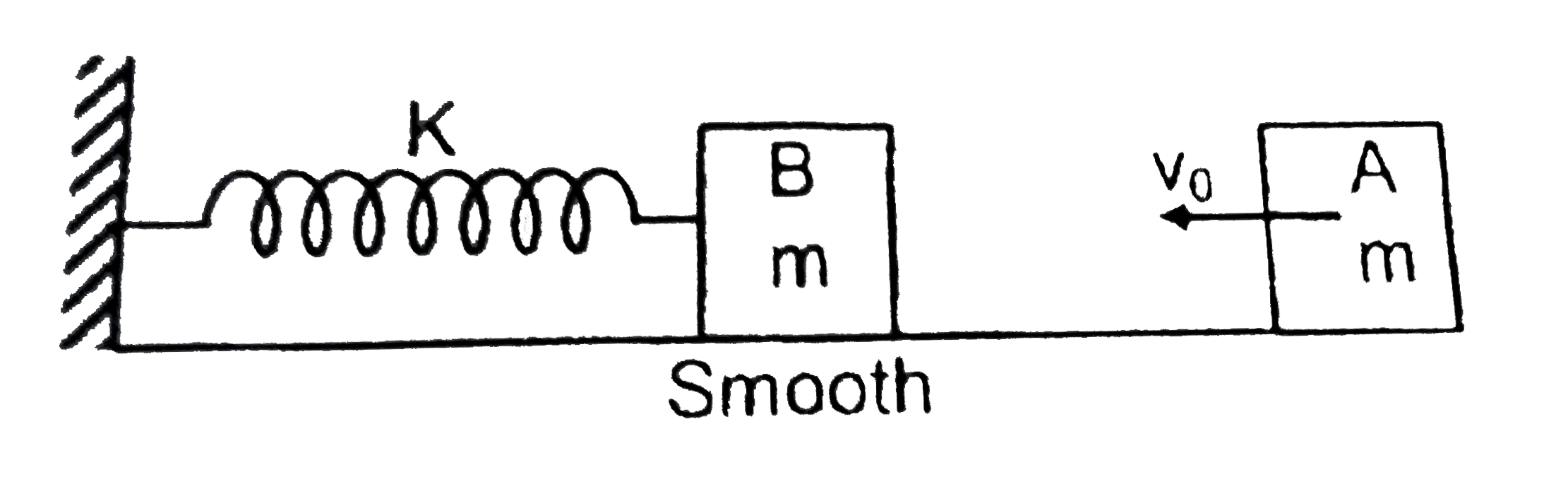
A block A of mass m is give a velocity v0 towards another block B of sae mass B. Is attached to an ideal spring of spring constant K. A makes a head on perfectly inelastic collision with B.
Answer the following two questions:
Q. Choose the correct option (s)View Solution
A block A of mass m is give a velocity v0 towards another block B of sae mass B. Is attached to an ideal spring of spring constant K. A makes a head on perfectly inelastic collision with B.
Answer the following two questions:
Q. Let the collision takes place at time t=0 choose the instant (s), when the spring is in its natural length.View SolutionThere are two identical particles A and B. One is projected vertically upward with speed √2gh from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of √hg.
View Solution

