A smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.

√3a2lω
√alω
√3alω
√3alω
The correct Answer is:A
Problem can be solved in rotatory frame. In disturbed condition:
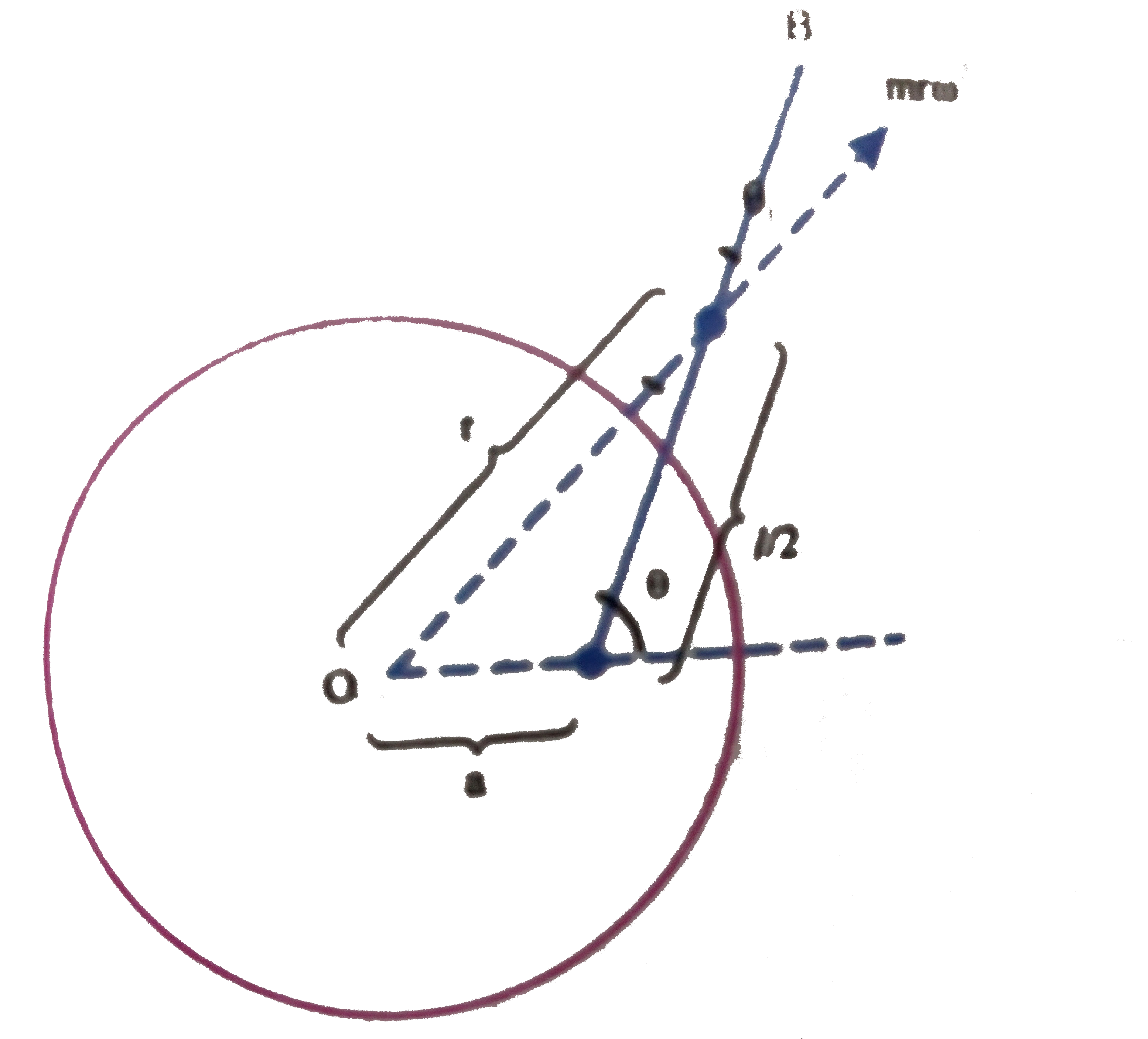
From diagram:
asinr=rsin(π−θ)⇒r=asinθsinr……….(1)
∴ torque about A is τ=−mrω2(l2sinθ1)........(2)
τ=Iα=ml23α........(3)θ is small.
Solve for angular frequency, ω0=?
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
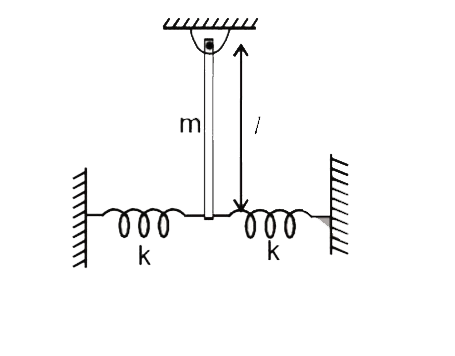
Find out the angular frequency of small oscillation about axis O
View SolutionA homogeneous disc of weight W and radius R rotates about the vertical axis OZ, the initial angular velocity being ω0. During the motion, the brake block A is pressed to the disc,with a radial force N for t0 seconds and the disc comes to rest because of friction. Find the coefficient of friction.
View Solution
Knowledge Check
A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
A2π√RgB2π√2RgC2π√2π3gD2π√3R2gA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
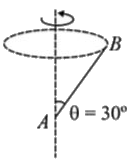 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA smooth horizontal disc rotates with a constant angular velocity ω about a stationary vertical axis passing through its centre, the point O. At a moment t=0 a disc is set in motion from that:
point with velocity v0. Find the angular momentum M(t) of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
View SolutionA horizontal disc rotating about a vertical axis passing through its centre makes 180 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 8 cm from its axis. If the frequency is thus reduced to 150 rpm, calculate the moment of inertia of the disc.
View Solution
