A graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The $y - and z - c o m p o \neq n t s$ of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is

A

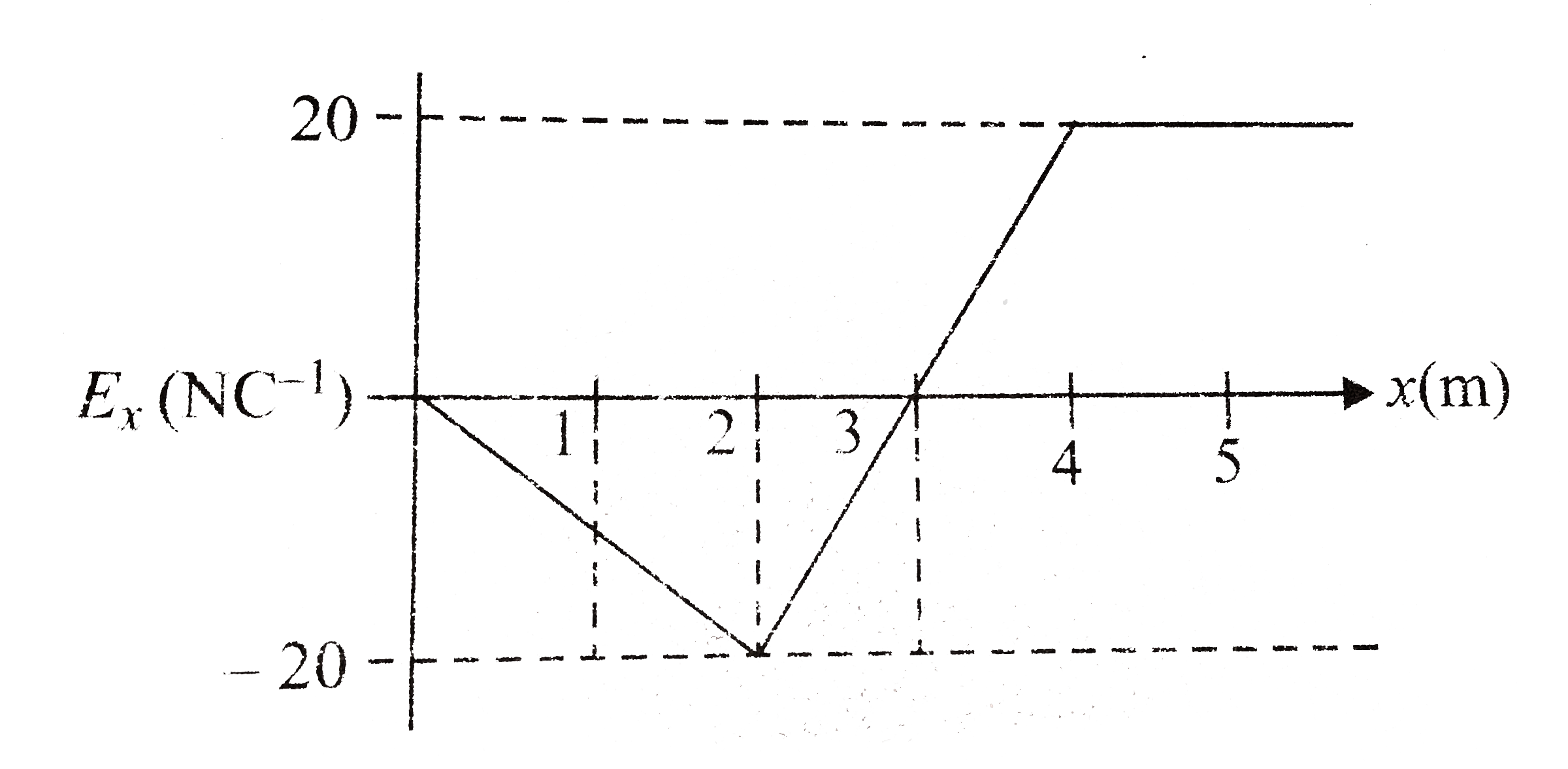
$10 V$

B

$40 V$

C

$- 10 V$

D

$30 V$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$V_{B} - V_{A} = - \int E_{x} d x$
$= - [Area under$ E_(x)-x $c u r v e]$
$V_{B} - 10 = - \frac{1}{2} .2 . (- 20) = 20 V_{B} = 30 V$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the electric field in region II as shown in figure.

Azero
B $\frac{σ}{4 π ε_{0}}$
C $\frac{σ}{ε_{0}}$
DInfinite
Question 2 - Select One
In a certain region of space, the electric field is zero. From this, we can conclude that the electric potential in this region is:
AConstant
BZero
CPositive
DNegative
Question 3 - Select One
In an electric field region, the electric potential varies along the x-axis as shown in the graph. The $x$ components of the electirc field in the regions for the intervals $P Q$ and $Q R$ as market in the garph, in $N / C$ , are respectively:

A $5.0$ along negative $x$ -direction and $20.0$ along positive x-direction
B $5.0$ along positive $x$ -direction and $20.0$ along negative $x$ -direction
C $5.0$ along negative $x$ -direction and $20.0$ along negative $x$ -direction
D $5.0$ along positive $x$ -direction and $20.0$ along positive x-direction

NARAYNA-ELECTROSTATICS AND GAUSS LAW-Level V

Home
Ask Doubt
Profile