A bullet of mass m and charge q is fired towards a solid uniformly charged sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum speed u so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrostatic forces )
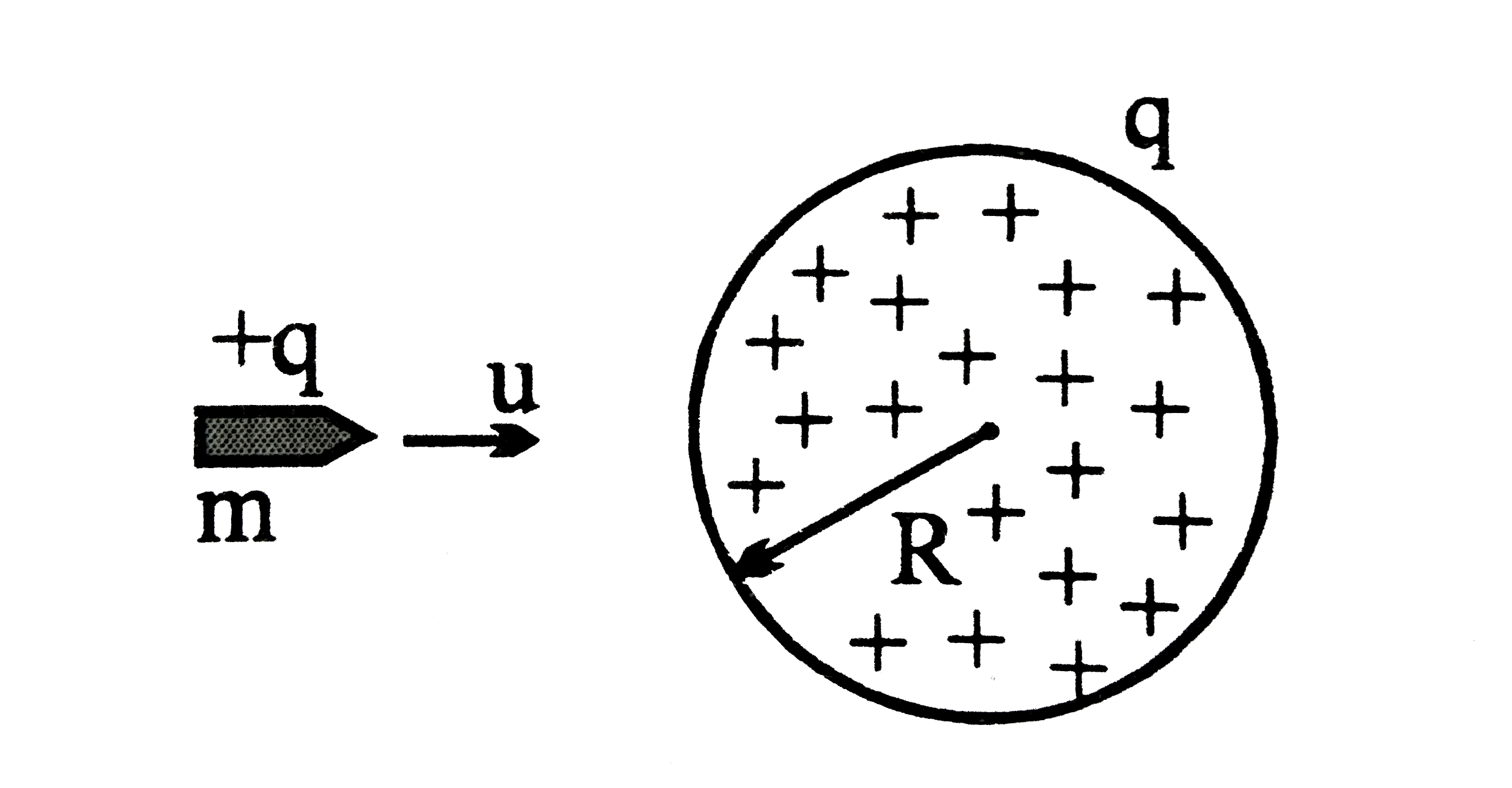 .
.
q√2πε0mR
q√4πε0mR
q√8πε0mR
√3q√4πε0mR
The correct Answer is:B
(TE)surface=(PE)centre Velocity of centre is nearly zero then it can across the sphere
14πε0q.qR+12mv2=32(14πε0qR)
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage I
3 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Passage II
3 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - NCERT based Question
14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View Solution
Knowledge Check
A bullet of mass m and charge q is fired towards a solid unifromly charged sphere of redius R and total cbharge +q. If it strikes the surface of sphere with speed u, find the minimum speeed u so that it can penetrate through the sphere , (Neglect all resistance forces or friction acting on bullet except electrositatic forces )
 .Aq√2πɛ0mRBq√4πɛ0mRCq√8πɛ0mRD(sq)rt3q√4πɛ0mR
.Aq√2πɛ0mRBq√4πɛ0mRCq√8πɛ0mRD(sq)rt3q√4πɛ0mRA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
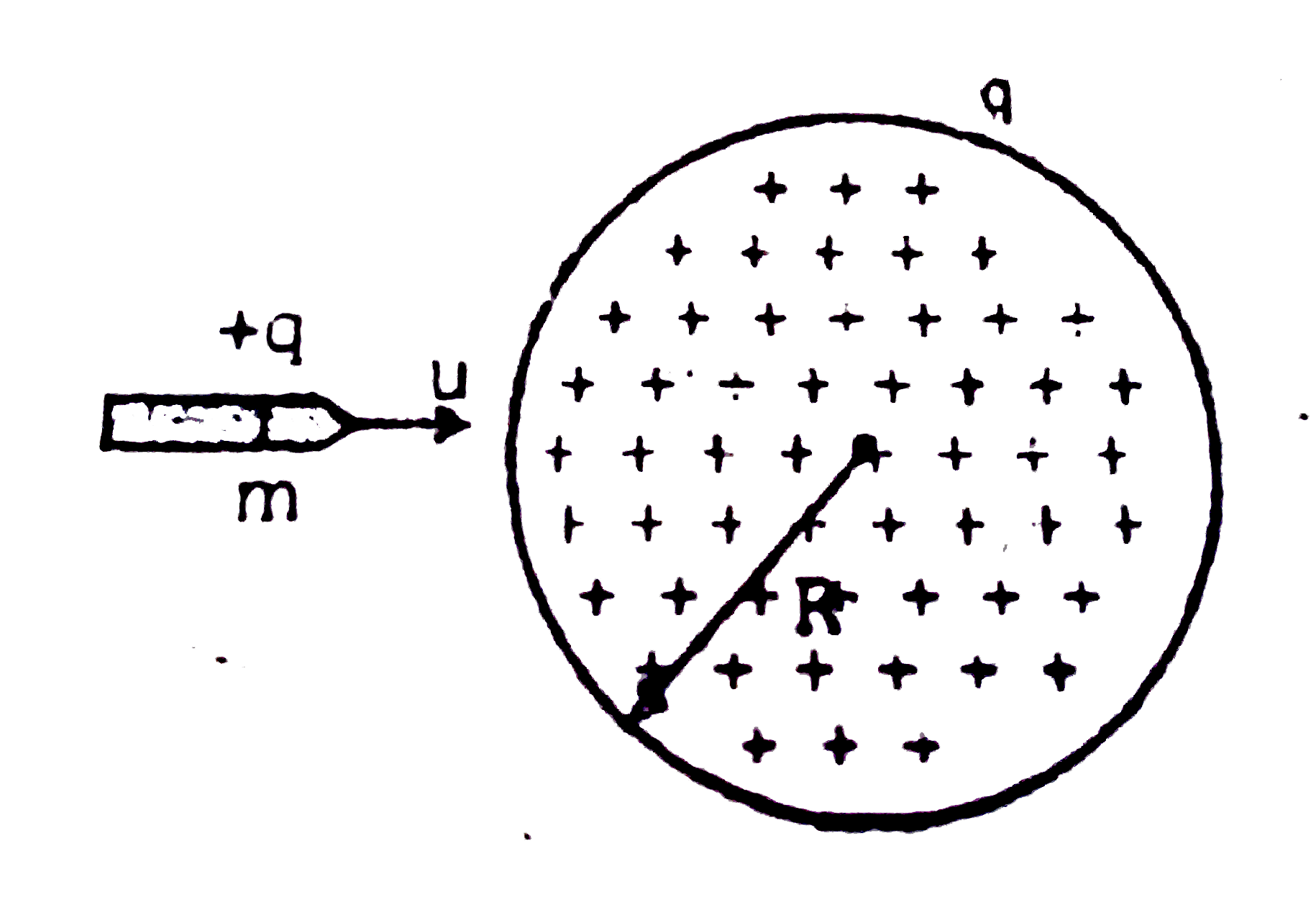 Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mR
Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mRA particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
A√14πε0qQmRB√14πε0qQmR2C√14πε0qQmR3D√14πε0mqQ
Figure shows a uniformly charged sphere of radius R and total charge Q. A point charge q is situated outside the sphere at a distance r from centre of sphere. Find out the following :
(i) Force acting on the point charge q due to the sphere.
(ii) Force acting on the sphere due to the point charge.

View SolutionIn a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U0 joules then find out self energy of sphere in term of U0 ?
View SolutionA conducting sphere of radius 2R carrying charge Q is joined to an uncharged conducting sphere of radius R. Find the charge flow through cinnecting wire.
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
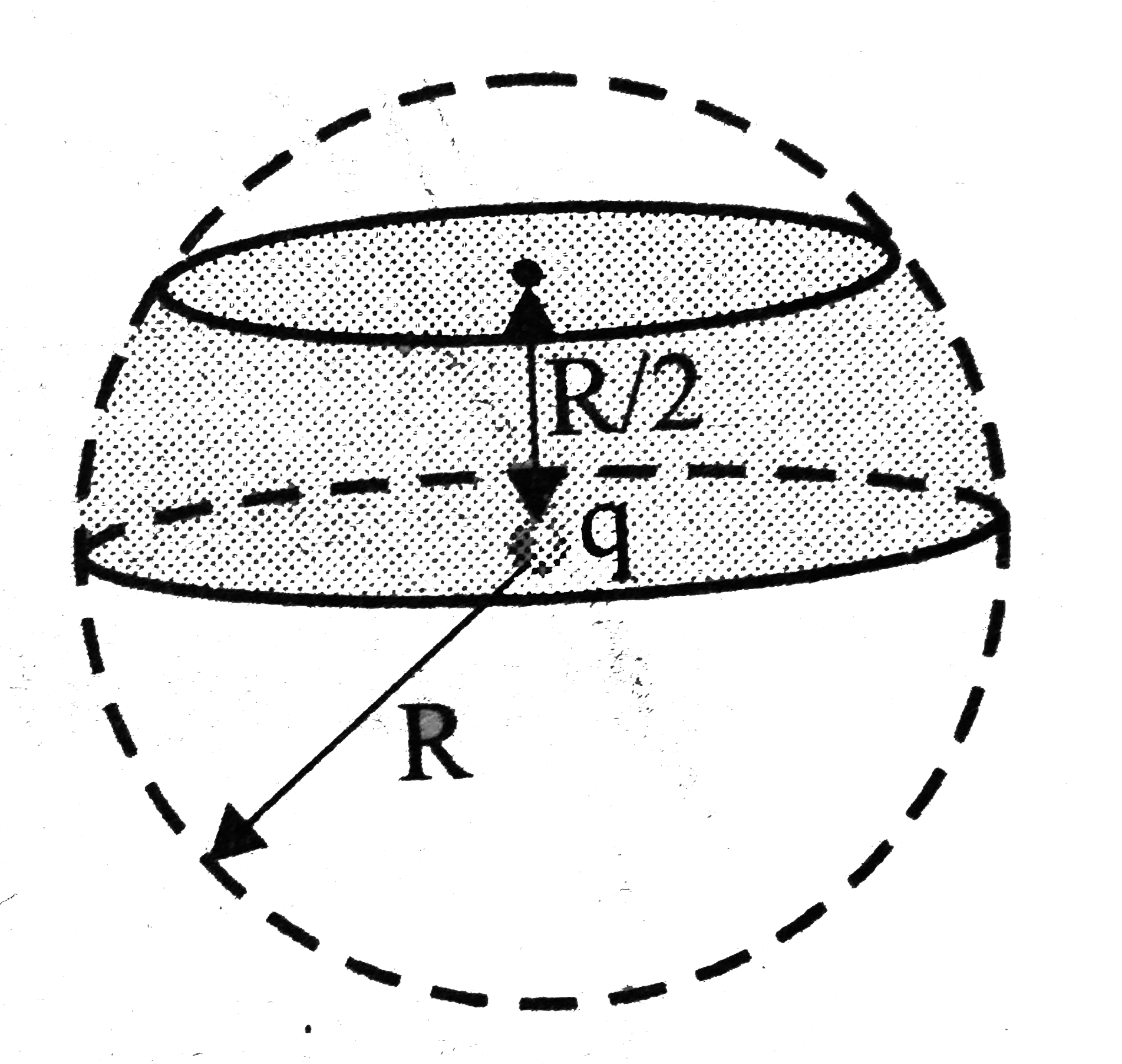
View Solution
