A conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.
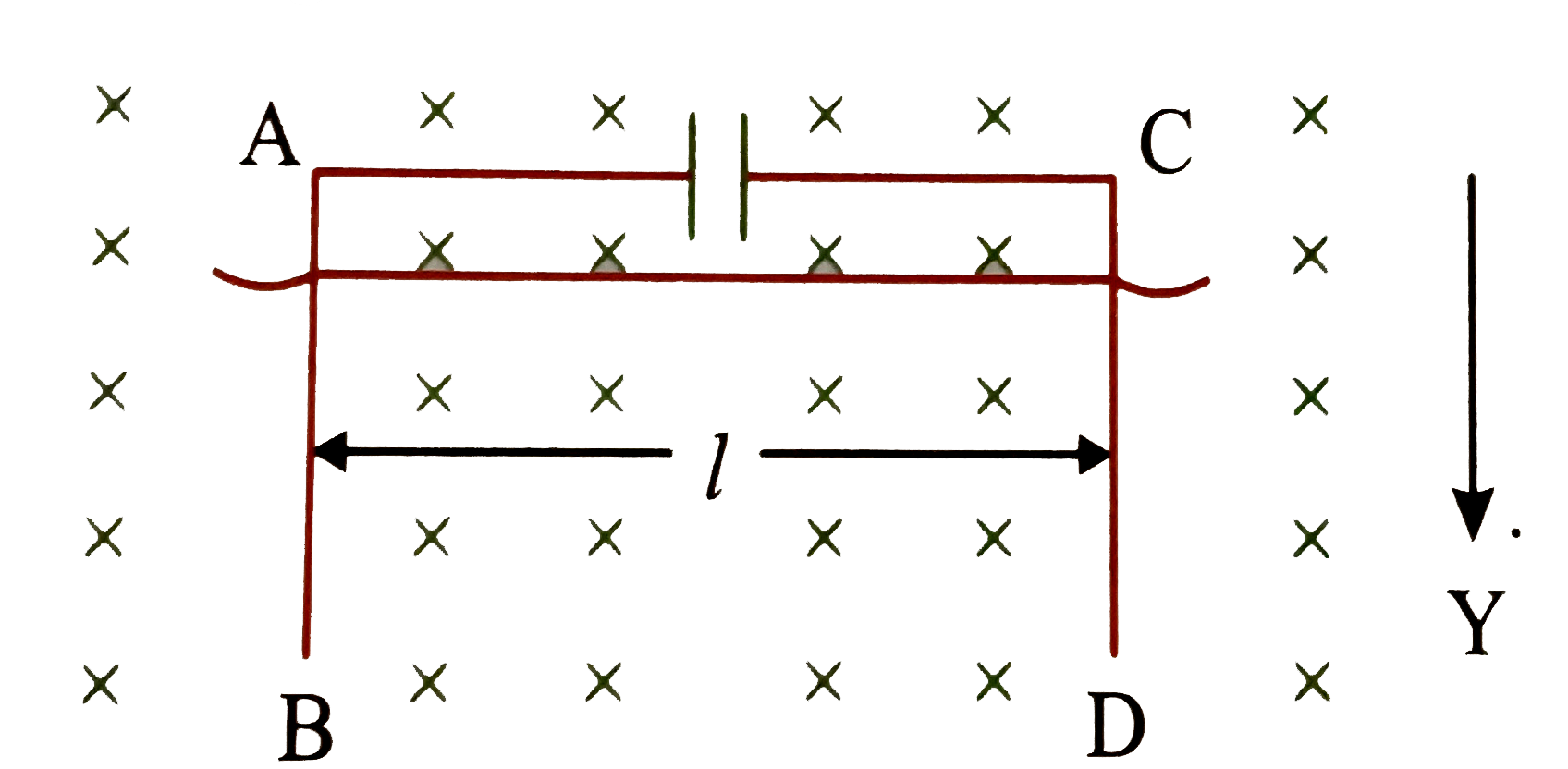
Based on above information answer the following questions:
Mark the correct statement about the motion of conductor
It is falling down with constant acceleration g
It is falling down with constant acceleration but not equal to g
It is falling down with increasing acceleration
It is falling down with decreasing acceleration
The correct Answer is:B
Let us say that in time t the conductor falls down by y and acquires a velocity v, then at this instant induced emf is
e=B0vl [with Q at higher potential]
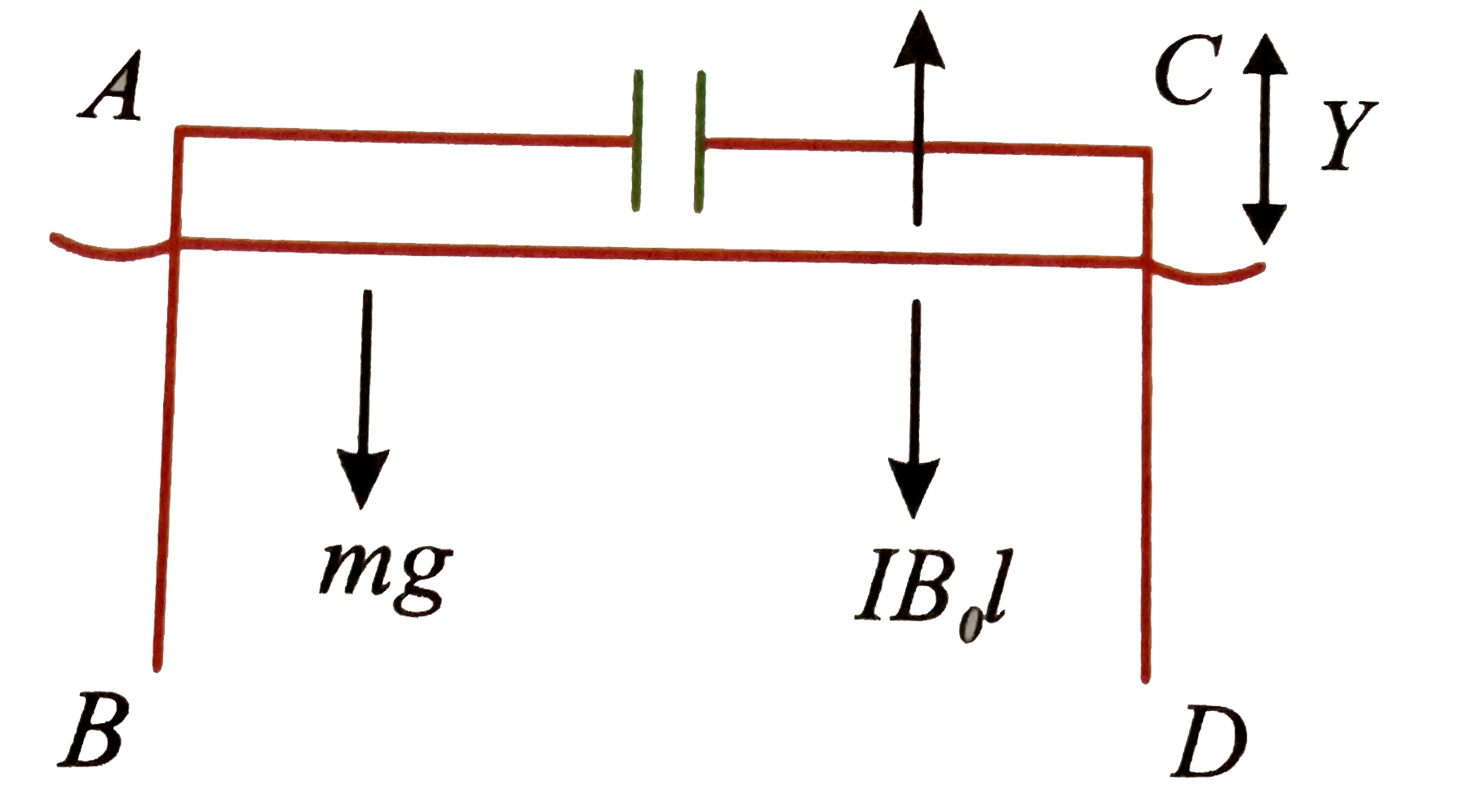
Charge on the capacitor at this instant is,
q=Ce=B0Cl×v
the current in the circuit at this instant is,
I=dqdt=B0Cldvdt=B0Cl×a
where a is the acceleration of the conductor at this instant.
Writing Newton's 2nd law equation for conductor,
mg−IB0l=ma
⇒a=mgm+CB20l2,
v=mgtm+CB20l2 and y=mgt22(m+CB20l2)
After solving above equations, we could have q as a function of y
as I=B0Cl×a
As a is constant, I is also constant.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -VI13videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Integer type questions2videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Single Answer Questions Level -V11videos
ELECTRO MAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -443videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)14videos
ELECTRO MAGNETIC WAVES
Similar Questions
A rectangular loop of wire with dimensions shown in figure is coplanar with a long wire carrying current 'I'. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
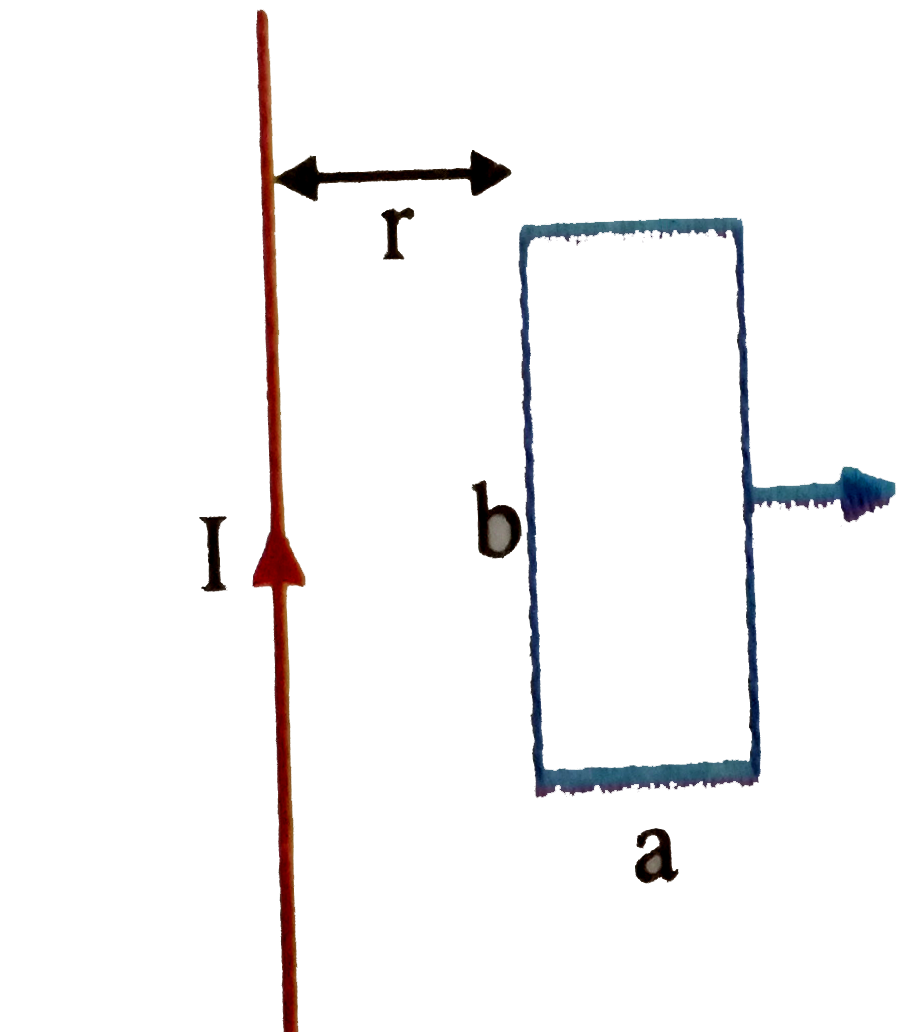 04:21View Solution
04:21View SolutionIn the figure, a conducting rod of length l=1 meter and mass m=1kg moves with initial velocity u=5m/s. On a fixed horizontal frame containing inductor L=2H and resistance R=1W. PQ and MN are smooth, conducting wires. There is a uniform magnetic field of strength B=1T. Initial there is no current in the inductor. Find the total charge in coulomb, flown through the inductor by the time velocity of rod becomes vf=1m/s and the rod has travelled a distance x=3 meter.
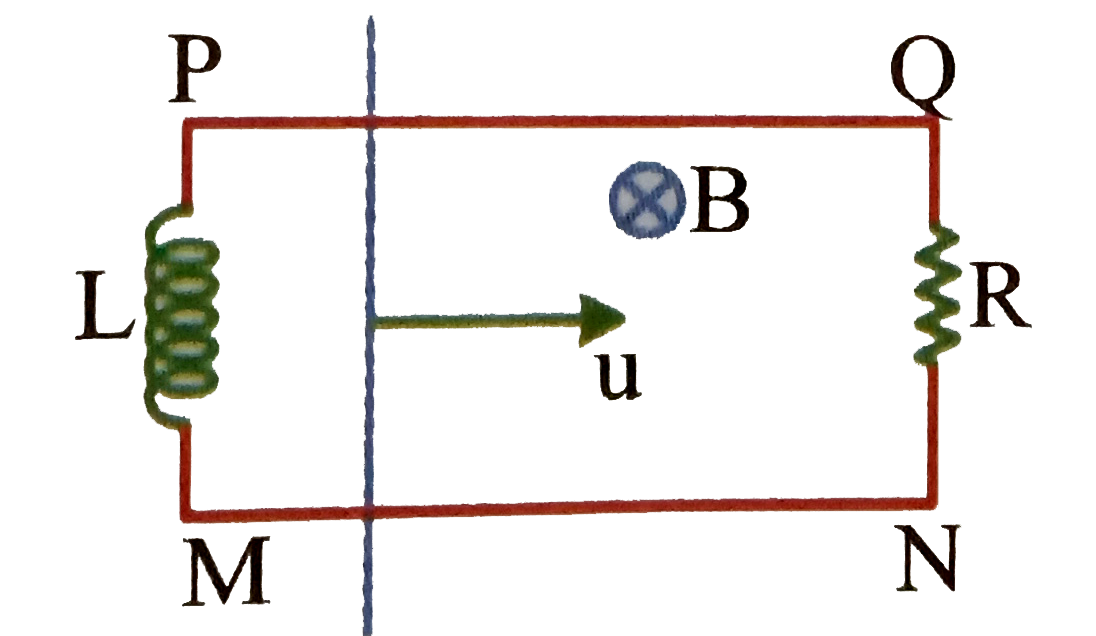 03:33View Solution
03:33View SolutionA helicopter has metallic blades with a length pf 3m extending outward from a central hub and rotating at 2rev/s. If the vertical component of the earht's magnetic field is 50μT, then the emf induced between the blade tip and the centre hub is
04:01View SolutionAn electron moving towards the east enters a magnetic field directed towards the north. The force on the electron will be directed
07:24View SolutionThe area of each plate of parallel plated condenser is 144cm2. The electrical field in the gap between the plates changes at the rate of 1012Vm−1s−1. The displacement current is
06:53View SolutionA conducting rod of length is moved at constant velocity v0 on two parallel, conducting, smooth, fixed rails, that are placed in a uniform constant magnetic field B perpendicular to the plane for the rails as shown in Fig. A resistance R is connected between the two ends of the rails.
Then which of the following is/are correct:
 02:13View Solution
02:13View SolutionAB and CD are fixed conducting smooth rails placed in a vertical palne and joined by a constant current source at its upper end. PQ is a conducting rod which is free to slide on the rails. A horizontal uniform magnetic field exists in space as shwn in figure. If the rod PQ is released from rest then,
06:24View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of
 04:47View Solution
04:47View SolutionA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C. The conductor is relased from rest when it is very close to AC i.e., y=0. A uniform magnetic field B0 perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g.

Based on above information answer the following questions:
Charge on the capacitor as a function of distance travelled y is given byView SolutionA conductor of mass m and length l is sliding smoothly an two vertical conducting rails AB and CD as shown in figure. The top ends of two conducting rails are joined by a capacitor of capacitance C . The conductor is relased from rest when it is very close to AC i.e., y = 0 . A uniform magnetic field B_(0) perpendicular to plane of figure existing. Neglect the resistance of rails and connecting wires. Take acceleration due to gravity to be g . Based on above information answer the following questions: Current in the circuit is
01:37View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
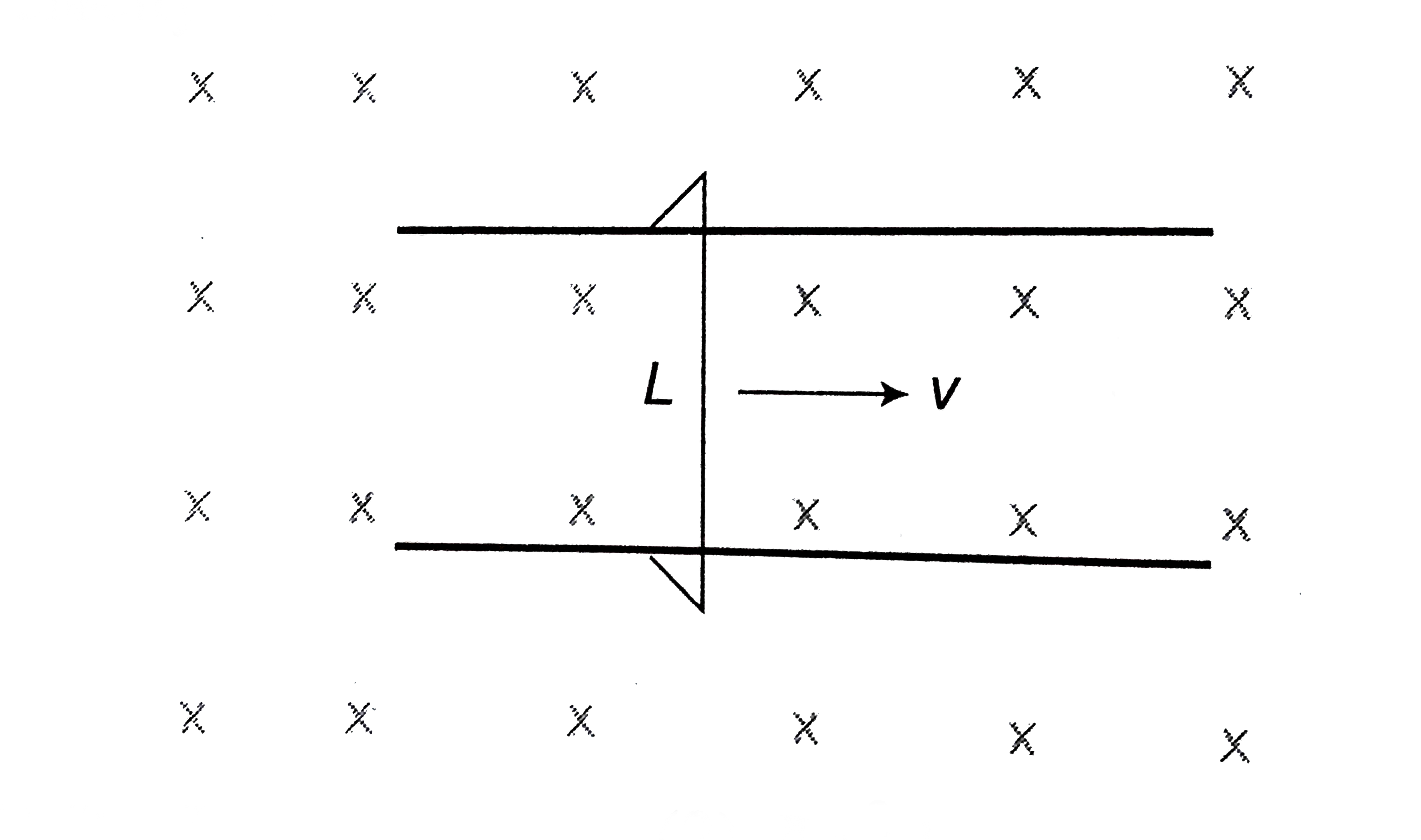 View Solution
View SolutionTwo long fixed parallel vertical conducting rails AB and CD are separated by a distance L. They are connected by resistance R and a capacitance C at two ends as shown in the figure. There is a uniform magnetic field B directed horizon- tally into the plane of the figure. A horizontal metallic bar of length L and mass m can slide without friction along the rails. The bar is released from rest at t = 0. Neglect resistance of bar and rails and also neglect the self inductance of the loop.
(a) Find the maximum speed acquired by the bar after it is released.
(b) Find the speed of the bar as a function of time t.
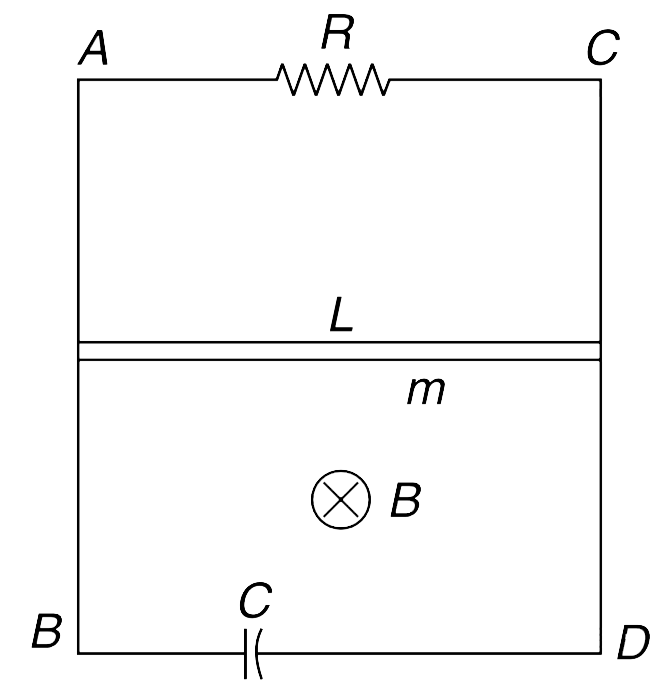 04:31View Solution
04:31View SolutionA straight horizontal conductor PQ of length l, and mass_ m slides down on two smooth conducting fixed parallel rails, set inclined at an angle 9 to the horizontal as shown in figure-5.30.
 The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 002:41View Solution
The top end of the bar are connected with a capacitor of capacitance C. The system is placed in a uniform magnetic field, in the direction perpendicular to the inclined plane formed by the rails as shown in figure. If the resistance of the bars and the sliding conductor are negligible calculate the acceleration of sliding conductor as a function of time ifit is released from rest at t= 002:41View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
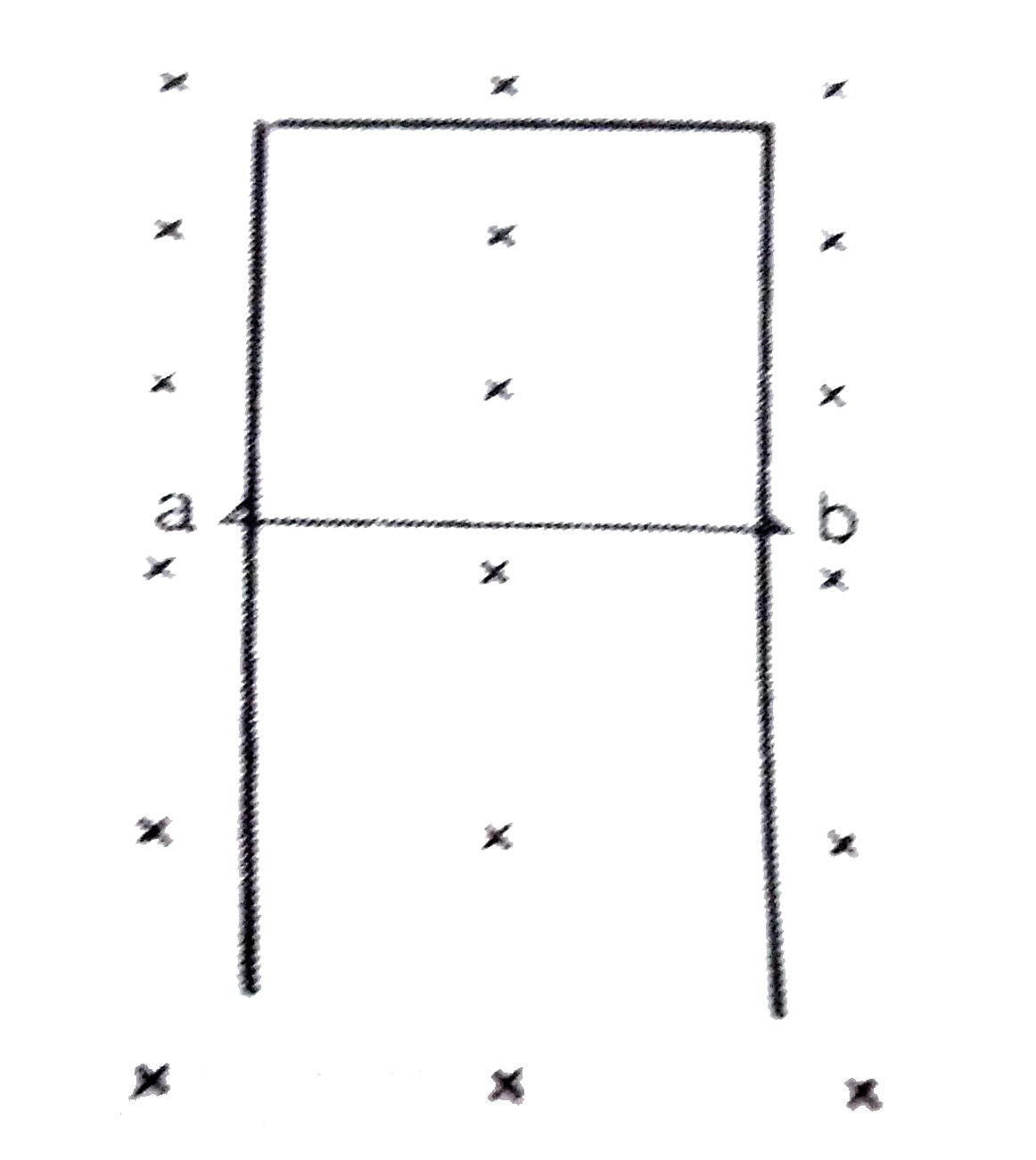 04:08View Solution
04:08View SolutionFigure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
 02:53View Solution
02:53View Solution

