In a ABC , ∠A=90o , AB=5cm and AC=12cm . If AD⊥BC , then AD= 132cm (b) 6013cm (c) 1360cm (d) 2√153cm
To solve the problem, we will follow these steps:
Step 1: Identify the triangle and given values
We have a triangle ABC where:
- ∠A=90∘ (right angle)
- AB=5cm
- AC=12cm
Step 2: Use the Pythagorean theorem to find BC
Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=52+122
BC2=25+144
BC2=169
Taking the square root:
BC=√169=13cm
Step 3: Calculate the area of triangle ABC
The area of triangle ABC can be calculated in two ways:
1. Using AB as the base and AC as the height:
Area=12×AB×AC=12×5×12=30cm2
2. Using BC as the base and AD as the height:
Area=12×BC×AD=12×13×AD
Step 4: Set the two area expressions equal to each other
Since both expressions represent the area of triangle ABC:
30=12×13×AD
Step 5: Solve for AD
Multiply both sides by 2 to eliminate the fraction:
60=13×AD
Now, divide both sides by 13:
AD=6013cm
Conclusion
The length of AD is:
AD=6013cm
Thus, the correct answer is (b) 6013cm.
---
We have a triangle ABC where:
- ∠A=90∘ (right angle)
- AB=5cm
- AC=12cm
Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
BC2=AB2+AC2
Substituting the values:
BC2=52+122
BC2=25+144
BC2=169
Taking the square root:
BC=√169=13cm
The area of triangle ABC can be calculated in two ways:
1. Using AB as the base and AC as the height:
Area=12×AB×AC=12×5×12=30cm2
Area=12×BC×AD=12×13×AD
Since both expressions represent the area of triangle ABC:
30=12×13×AD
Multiply both sides by 2 to eliminate the fraction:
60=13×AD
Now, divide both sides by 13:
AD=6013cm
The length of AD is:
AD=6013cm
Thus, the correct answer is (b) 6013cm.
Topper's Solved these Questions
Similar Questions
In a ABC, if AB=5cm,BC=13andCA=12cm , then the distance of vertex 'A' from the side BC in (in cm) a.2513 b. 6013 c. 6512 d. 14413
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=6cm , AC=5cm and BD=3cm , then DC= 11.3cm (b) 2.5cm (c) 3:5cm (d) None of these
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=8cm , BD=6cm and DC=3cm . Find AC 4cm (b) 6cm (c) 3cm (d) 8cm
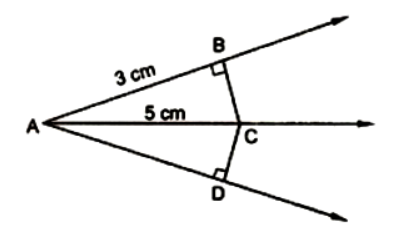
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
View SolutionXY is drawn parallel to the base BC of a ABC cutting AB at X and AC at Y . If AB=4 BX and YC=2cm , then AY= 2cm (b) 4cm (c) 6cm (d) 8cm
View SolutionABC is such that AB=3cm , BC=2cm and CA=2.5cm . If DEF~ABC and EF=4cm , then perimeter of DEF is (a) 7.5cm (b) 15cm (c) 22.5cm (d) 30cm .
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=

(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionLength of each edge, of a regular tetrahedron is 1 cm. Its volume is √312cm3 (b) 14√3 cm3 (c) √26cm3 (d) 112√2 cm3
View SolutionIf three A.M.s are inserted between b and c, then the mind A.M. is 112 (b) 132 (c) 152 (d) 172
View Solution
