In an equilateral triangle if , then (b) (c) (d)
To solve the problem, we will analyze the given equilateral triangle ABC with AD being the altitude from vertex A to side BC. Let's derive the relationship step by step.
Step 1: Understand the properties of the equilateral triangle
In an equilateral triangle, all sides are equal, and all angles are 60∘. Therefore, we have:
AB=BC=CA
Step 2: Identify the right triangle
Since AD is perpendicular to BC, triangle ABD is a right triangle with:
- AB as the hypotenuse
- AD as one leg
- BD as the other leg
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
AB2=AD2+BD2
Step 4: Determine BD
In an equilateral triangle, the altitude also bisects the base. Therefore:
BD=12BC
Since BC=AB in an equilateral triangle, we have:
BD=12AB
Step 5: Substitute BD into the Pythagorean theorem
Now substitute BD into the equation:
AB2=AD2+(12AB)2
This simplifies to:
AB2=AD2+14AB2
Step 6: Rearrange the equation
To isolate AD2, we can rearrange the equation:
AB2−14AB2=AD2
This simplifies to:
34AB2=AD2
Step 7: Express the relationship
Now, we can express this relationship in terms of squares:
3AB2=4AD2
Conclusion
Thus, the correct relationship is:
3AB2=4AD2
The answer is option (c).
---
In an equilateral triangle, all sides are equal, and all angles are 60∘. Therefore, we have:
AB=BC=CA
Since AD is perpendicular to BC, triangle ABD is a right triangle with:
- AB as the hypotenuse
- AD as one leg
- BD as the other leg
According to the Pythagorean theorem:
AB2=AD2+BD2
In an equilateral triangle, the altitude also bisects the base. Therefore:
BD=12BC
Since BC=AB in an equilateral triangle, we have:
BD=12AB
Now substitute BD into the equation:
AB2=AD2+(12AB)2
This simplifies to:
AB2=AD2+14AB2
To isolate AD2, we can rearrange the equation:
AB2−14AB2=AD2
This simplifies to:
34AB2=AD2
Now, we can express this relationship in terms of squares:
3AB2=4AD2
Thus, the correct relationship is:
3AB2=4AD2
The answer is option (c).
Topper's Solved these Questions
Similar Questions
In an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIf E is a point on side CA of an equilateral triangle ABC such that BE⊥CA , then AB2+BC2+CA2= 2 BE2 (b) 3 BE2 (c) 4 BE2 (d) 6 BE2
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionWith usual notations in a triangle ABC, if r1=2r2=2r3 then 4a=3b (b) 3a=2b 4b=3a (d) 2a=3b
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View SolutionMatch the following.
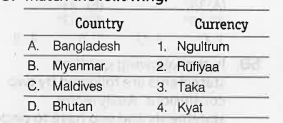
Codes A B C D
(A) 4 3 1 2 (B) 2 4 1 3 (C) 3 4 2 1 (D) 3 4 1 2
View Solution
