ABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2,
ABCD is a rectangle, and O is any point in its interior.
Area (△AOD)=3sqcm and Area △BOC=6sqcm.
From O draw a line EF∣∣AB intersecting ADat E and BCat F.
Therefore,OE⊥ADand OF⊥BC
Let OE=xand OF=y
OE+OF=EF=AB
Therefore x+y=AB ....(1)
ar△AOD+Area△BOC=3+6=9sq.cm.
12×AD×OE+12×OF×BC=9sq.cm
12(AD×OE+OF×BC)=9sq.cm
(AD×OE+OF×BC)=9×2=18sqcm
Since BC=AD (opposite sides of a rectangle)
⇒AD(OE+OF)=18sq.cm
AD×EF=18sq.cm
So, EF=AB
⇒AD×AB=18sq.cm
Area of the rectangle ABCD=AB×AD=18sq.cm
Topper's Solved these Questions
Similar Questions
Medians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (ABGC)= 6 cm2 (b) 9 cm2 (c) 12 cm2 (d) 18cm2
View SolutionABCD is a parallelogram. P is any point on CD. If ar (DPA)=15 cm2 and ar (APC)=20cm2, then ar (APB)=
(a) 15cm2 (b) 20cm2 (c) 35 cm2 (d) 30cm2View SolutionThe area of a circle is 220 cm2 . The area of a square inscribed in it is (a) 49 cm2 (b) 70 cm2 (c) 140 cm2 (d) 150 cm2
View SolutionABCDEF , ar(ABC)=9cm2 , ar(DEF)=16cm2 . If BC=2.1cm , then the measure of EF is 2.8cm (b) 4.2cm (c) 2.5cm (d) 4.1cm
View SolutionIf the diagonal of a rectangle is 17 cm and its perimeter is 46 cm, the area of the rectangle is (a)100cm2 (b) 110cm2 (c)120 cm2 (d) 240 cm2
View SolutionIn a ABC if D and E are mid-points of BC and AD respectively such that ar (AEC)=4 cm2 , then ar (BEC)= 4 cm2 (b) 6 cm2 (c) 8 cm2 (d) 12cm2
View SolutionLet ABCD be a parallelogram and ABEF be a rectangle with EF lying along the line CD . If AB=7cm and BE=6.5cm , then the area of the parallelogram is 11.375cm2 (b) 22.75cm2 (c) 45cm2 (d) 45.5cm2
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
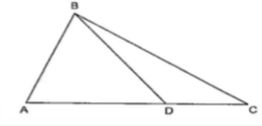
View SolutionIn Figure, the ratio ofAD to DC is 3:2. If the area of ΔABC is 40cm2, what is the area of ΔBDC? (a)16cm2 (b) 24cm2 (c) 30cm2 (d) 36cm2
 View Solution
View Solution

