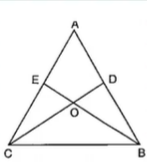
In Figure, AB=CD. Prove that BE=DE and AE=CE, where E is the point of intersecting of AD and BC.
Step by step video & image solution for In Figure, A B=C Ddot Prove that B E=D E\ a n d\ A E=C E , where E is the point of intersecting of A D\ a n d\ B Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
D and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionIn Figure, BE⊥AC, AD is any line from A → BC intersecting BE in H.P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE

View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)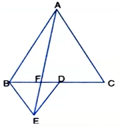
View Solution
