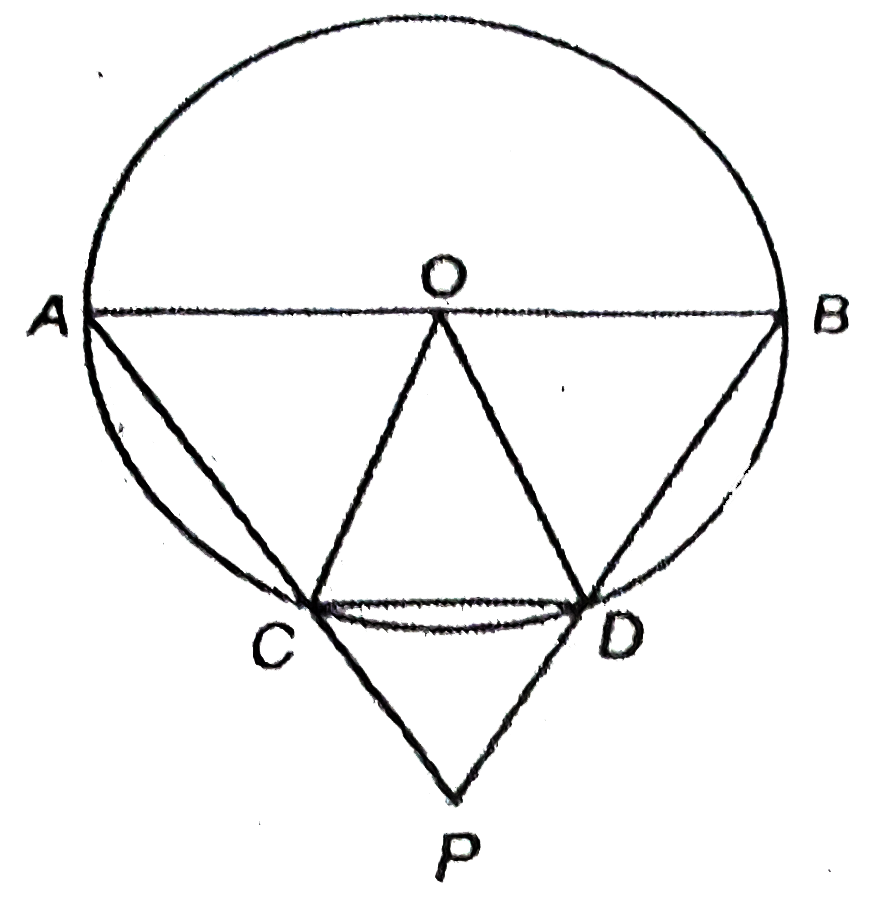
In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal t

AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the $∠ A E B$ .
A $30^{\circ}$
B $60^{\circ}$
C $90^{\circ}$
D $45^{\circ}$
AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of $∠ A P B$ is:
A $120^{\circ}$
B $30^{\circ}$
C $60^{\circ}$
D $90^{\circ}$
AB is a diameter of the circle with centre $O$ and chord $C D$ is equal to radius $O C$ (fig). $A C$ and $B D$ proudced meet at P. Prove that $∠ C P D = 60^{\circ}$ .

A $60^{\circ}$
B $30^{\circ}$
C $90^{\circ}$
D $160^{\circ}$

In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that $∠AEB\ =\ 60∘$