ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
Solution:
∠ABC=∠ADC
△ABC and △ADC lie on the same semi circle and on a common diameter AC
A,B,C, and D are concyclic
CD is a chord
∴∠CAD=∠CBD(The angle made by a chord on the same segment are equal)
Hence Proved.
Topper's Solved these Questions
Similar Questions
In Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
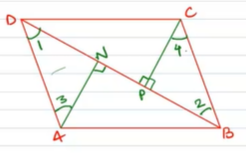 View Solution
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=90∘ (iii)DBC≅ACB (iv) CM=12AB
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionTriangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABC is a triangle. D is the mid point of BC. If AD is perpendicular to AC, then prove that cosA .cosC=2(c2−a2)3ac .
View SolutionBisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
View Solution

