In Figure, if ∠DBC=700 and ∠BAC=300, find ∠BCD. Further, if AB=BC, find ∠ECD
Step by step video & image solution for In Figure, if /_D B C=70^0\ a n d\ /_B A C=30^0,\ find /_B C Ddot Further, if A B=B C , find /_E C D by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70o,∠BAC is 30o, find ∠BCD. Further, if AB = BC, find∠ECD.
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
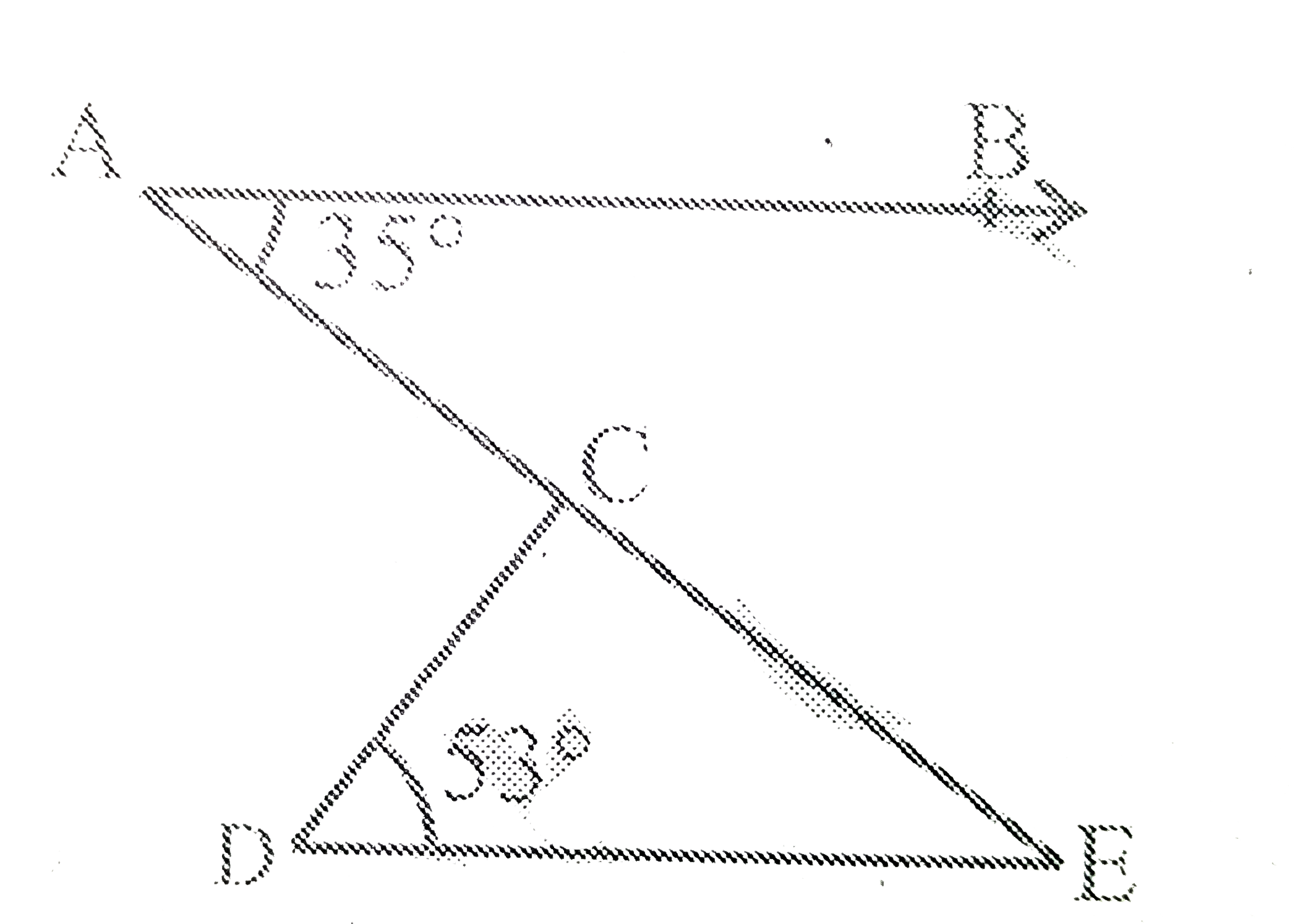
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIf ABCD is a rectangle with ∠BAC=32∘, find the measure of ∠DBC
View SolutionIn a ΔABC, if b=√3, c=1 and ∠A=300, then find a
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View SolutionIn Figure, if EC∣∣AB, ∠ECD=700AND ∠BDO=200 , then ∠OBD is: 200 (b) 500 (c) 600 (d) 700
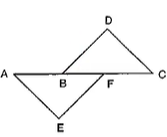
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View Solution
