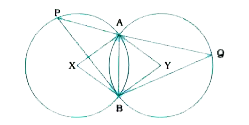
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP=∠QCD .
We conclude from the given information that Chords AP and DQ are joined.
⇒In chord AP,
⇒∠PBA=∠ACP ..... (Angles on the same segment --- .........(i)
Similarly
=> In chord DQ,
⇒∠DBQ=∠QCD ...Angles on the same line segment)....... (ii)
⇒ABD and PBQ are line segments intersecting at B.
⇒∠PBA=∠DBQ ...Vertically opposite angles --- (iii)
By the equations (i), (ii) and (iii),
∠ACP=∠OCD
Hence proved.
Topper's Solved these Questions
Similar Questions
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionIn the given figure two circles intersect at two points B and C. Two line segments ABD and PBQ passing through point B, intersects circles respectively at A, D and P, Q . Prove that ∠ACP=∠QCD
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
A1.50cmB2.25cmC4.50cmD9.00cm
In figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.
 View Solution
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAS is drawn so that P, Olie on the two circles. Prove that BP = BQ.
 View Solution
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.
 View Solution
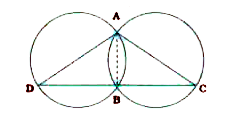
View SolutionTwo circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
 View Solution
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionTwo circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View Solution

