
A mass of mass 60 kg hangs himself from a massless spring balance. Which itself suspneded from an ideal string-pulley system as shown in the figure. The stirng AB can bear maximum 900 N. Choose correct statement.
The man is never ever able to read his correct weight in the spring balance.
If man is able to manage himself at rest, the spring balance reads his true weight.
The maximum magnitude of accelerationman can manage is 12.5 while moving upward.
When man moves downward with acceleration the spring balance will read 40 kg.
The correct Answer is:C
..(i)
2T=kx
Reading of spring balance
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
Consider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
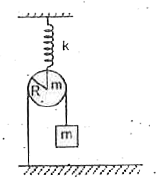 View Solution
View Solution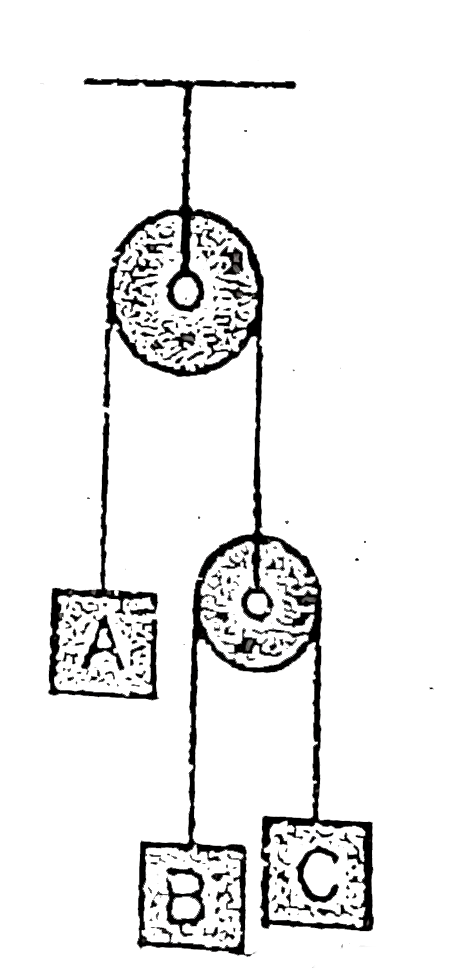
Three blocks A, B and C havig masses m kg, 2kg and 3 kg are attached by massless strings and ideal pulleys as shown in the figure. When the system is realeased from rest if the block A remains stationary. the mass of block A isView Solution
Knowledge Check
- Question 1 - Select One

An ideal string pulley system is shown in the figure and system is released from rest choose correct optionAWhen mass B moves with speed 4m/s the speed of mass A is 1 m/sBWhen mass B moves with speed 1m/s, the speed of mass A is 4m/sCIn the time interval in which the mass A covers distance 8 m, in the same time interval, mass B travels a distance 1m.Din the time interval in which the mass A covers distance 1m, in the same time inverval, mass B travels a distance 8 m. - Question 2 - Select One
A mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
A10√3 kg wtB20√3 kg wtC20 kg wtD10 kg wt - Question 3 - Select One
A mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
A20 kg-wtB10 kg-wtC10√3 kg-wtD20√3 kg-wt
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
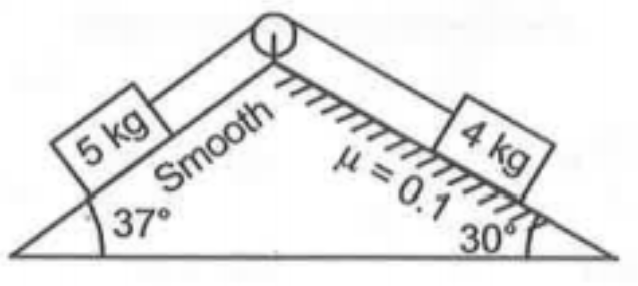 View Solution
View SolutionA mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground
 View Solution
View SolutionTwo blocks A and B having masses 5 kg and 10 kg respectively connected through a massless string which is passing over a pulley (disc) of mass 2 kg and radius 25 cm as shown in figure If system is. released from rest. then angular acceleration of the pulley is (String does not slip over the pulley horizontal surface is smooth and g=10ms−2
View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring constant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .
 View Solution
View SolutionA trolley of mass 20 kg is attached to a block of mass 4kg by massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the acceleration of the trolley and block system is (Takeg=10ms−2)
 View Solution
View Solution

