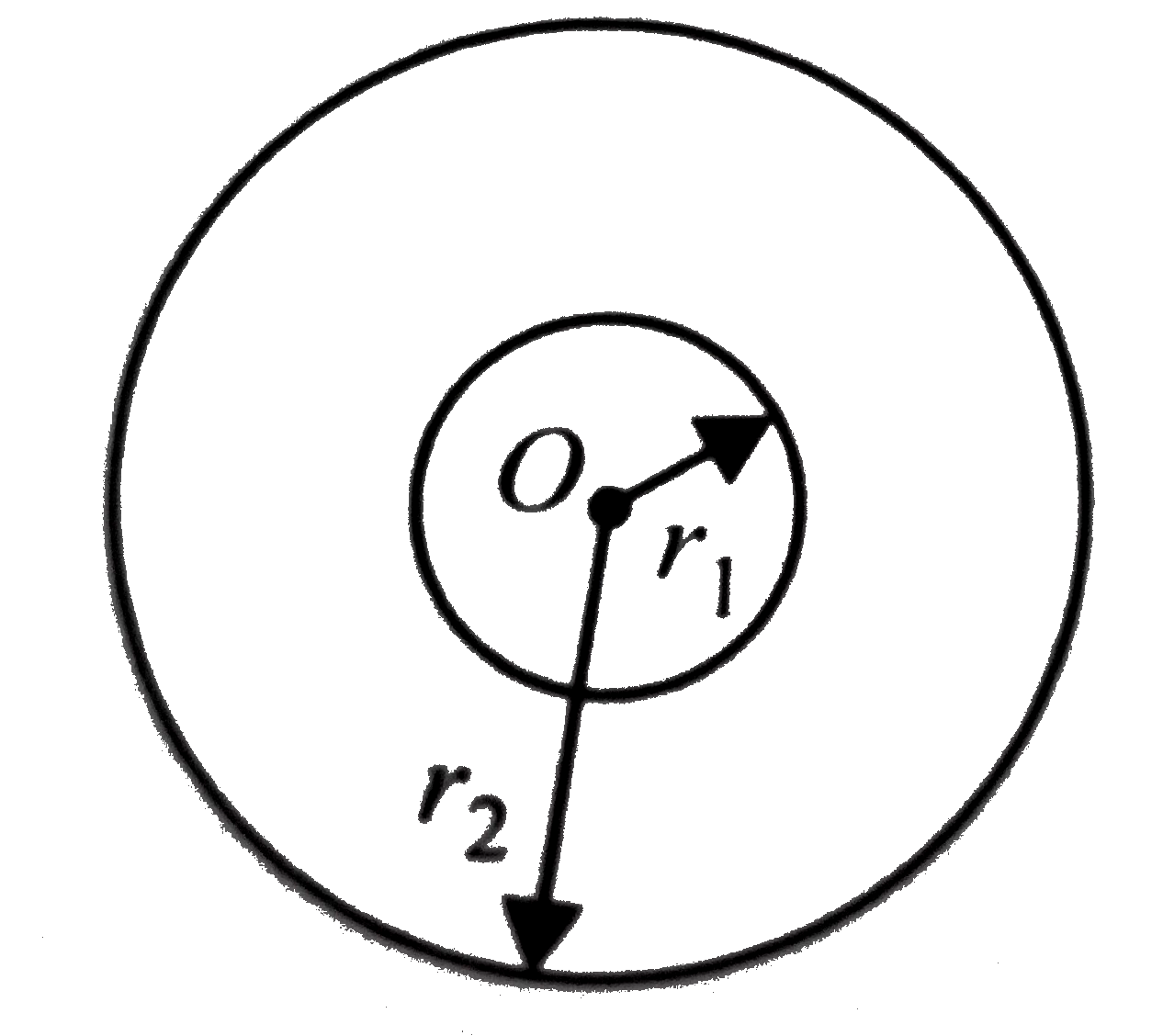
Two thin conectric shells made of copper with radius $r_{1}$ and $r_{2} (r_{2} > r_{1})$ have a material of thermal conductivity $K$ filled between them. The inner and outer spheres are maintained at temperature $T_{H}$ and $T_{C}$ respectively by keeping a heater of power $P$ at the centre of the two sphers. Find the value of $P$ .

Text Solution

Verified by Experts

Heat flowing per second through each cross-section of the sphere $= P = i$ . Thermal resistance of the spherical sheel of radius $x$ and thickness $d x$ .
$d R = \frac{d x}{K .4 π x^{2}}$
$\Rightarrow R = r_{2} \int r_{1} \frac{d x}{4 π x^{2} K} = \frac{1}{4 π K} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$
thermal current
$i = P = \frac{T_{H} - T_{C}}{R} = \frac{4 π K (T_{H} - T_{C}) r_{1} r_{2}}{(r_{2} - r_{1})}$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Space between tow concentric spheres of radii $r_{1} and r_{2}$ such that $r_{1} < r_{2}$ is filled with a material of resistivity $ρ$ . Find the resistance between inner and outer surface of the material

A $\frac{r_{1}}{r_{2}} \frac{p}{2}$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}} \frac{p}{4 π}$
C $\frac{r_{1} r_{2}}{r_{2} - r_{1}} \frac{p}{4 π}$
Dnone of these.
Question 2 - Select One
Space between tow concentric spheres of radii $r_{1} and r_{2}$ such that $r_{1} < r_{2}$ is filled with a material of resistivity $ρ$ . Find the resistance between inner and outer surface of the material

A $\frac{r_{1}}{r_{2}} \frac{p}{2}$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}} \frac{p}{4 π}$
C $\frac{r_{1} r_{2}}{r_{2} - r_{1}} \frac{p}{4 π}$
Dnone of these.
Question 3 - Select One
Consider two concentric spherical metal shells of radii $r_{1}$ and $r_{2} (r_{2} > r_{1})$ . If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A $\frac{- r_{2}}{r_{1}} q$
Bzero
C $\frac{- r_{1}}{r_{2}} q$
D $- q$

RESONANCE-HEAT TRANSFER-Example

Home
Ask Doubt
Profile