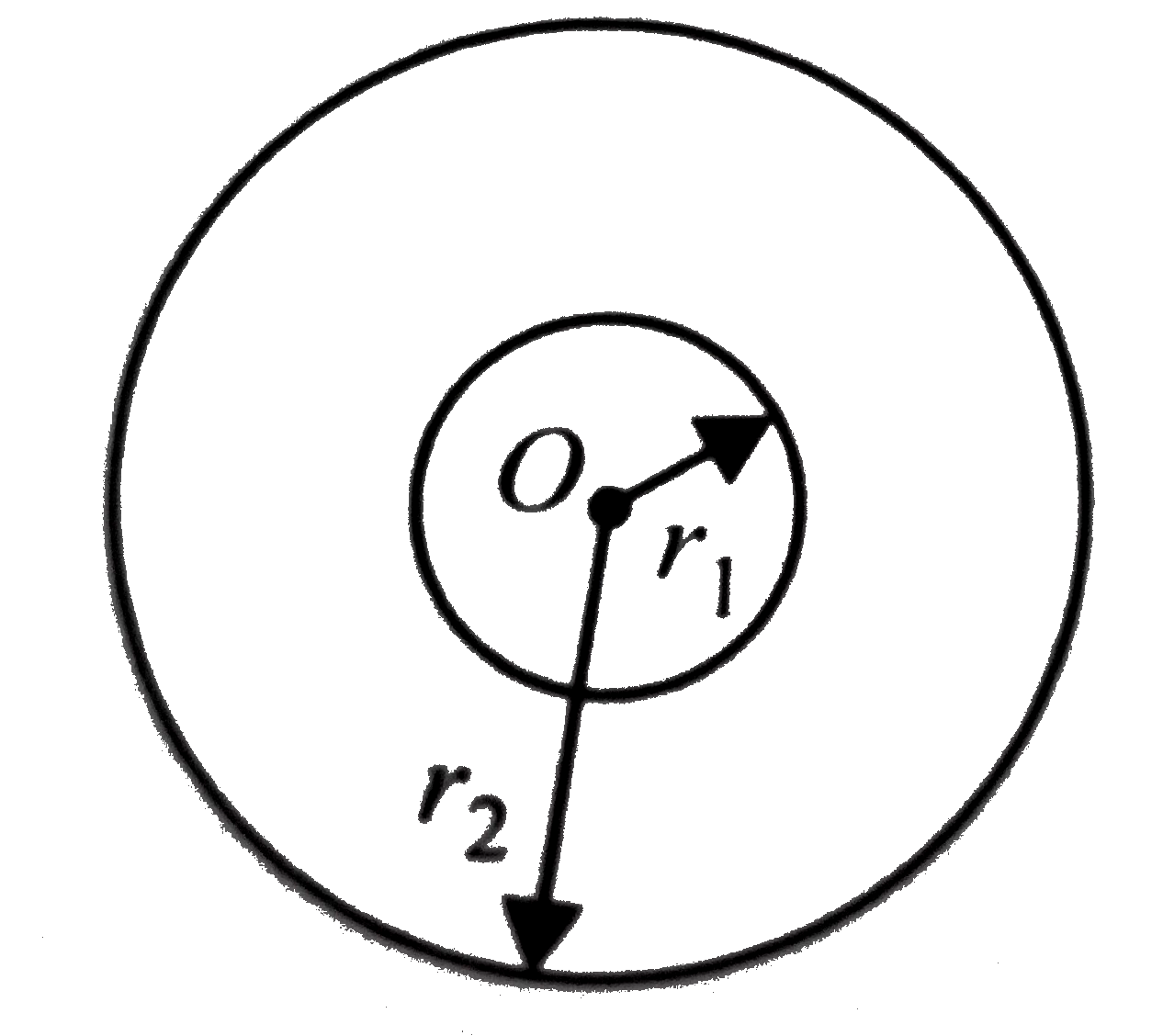
Two thin metallic spherical shells of radii $r_{1} and r_{2} (r_{1} < r_{2})$ are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature $θ_{1}$ .and the outer shell at temperature $θ_{2} (θ_{1} < θ_{2})$ . Calculate the rate at which heat flows radially through the material.

Video Solution

Text Solution

Verified by Experts

Let us drow two spherical shells of radii x and $x + d x$ concentric with the given system. Let the temperatures at these shells be theta and $θ + d t h η$ respectively. The amount of heat flowing radially inward through the material between x and $x + d x$ is
$\frac{Δ Q}{Δ t} = \frac{K 4 π x^{2} d θ}{d x}$ . thus, $K 4 π \int_{θ_{1}}^{θ_{2}} d θ = \frac{Δ Q}{Δ t} \int_{r 1}^{R 2} \frac{d x}{x^{2}}$ . or, $K 4 π (θ_{2} - θ_{1}) = \frac{Δ Q}{Δ t} (\frac{1}{R_{1}} - \frac{1}{R_{2}})$ . or, (DeltaQ)/(Deltat)=(4piKr_(1)r_(2)(theta_(2)-theta_(1)))/(r_(2)-r_(1))

Updated on:21/07/2023

The capacitance of two concentric spherical shells of radii $R_{1}$ and $R_{2} (R_{2} > R_{1})$ is
A $4 π ε_{0} R_{2}$
B $4 π ε_{0} \frac{(R_{2} - R_{1})}{R_{1} R_{2}}$
C $4 π ε_{0} \frac{R_{1} R_{2}}{(R_{2} - R_{1})}$
D $4 π ε_{0} R^{1}$
Consider two concentric spherical metal shells of radii $r_{1}$ and $r_{2} (r_{2} > r_{1})$ . If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A $\frac{- r_{2}}{r_{1}} q$
Bzero
C $\frac{- r_{1}}{r_{2}} q$
D $- q$
Space between tow concentric spheres of radii $r_{1} and r_{2}$ such that $r_{1} < r_{2}$ is filled with a material of resistivity $ρ$ . Find the resistance between inner and outer surface of the material

A $\frac{r_{1}}{r_{2}} \frac{p}{2}$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}} \frac{p}{4 π}$
C $\frac{r_{1} r_{2}}{r_{2} - r_{1}} \frac{p}{4 π}$
Dnone of these.