Two thin concentric shells made from copper with radius $r_{1} and r_{2} (r_{2} > r_{1})$ have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperatures $T_{H} and T_{C}$ respectively by keeping a heater of power P at the centre of the two spheres. Find the value of P.

Video Solution

Text Solution

Verified by Experts

Heat flowing per second through each cross-section of the sphere $= P = i$
Thermal resistance of the spherical shell of radius x and thickness dx.
$d R = \frac{d x}{K .4 π x^{2}}$
$\Rightarrow R = r^{2} \int r_{1} \frac{d x}{4 π x^{2} . K} = \frac{1}{4 π K} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$
thermal current

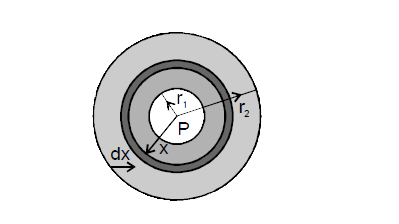
$i = P = \frac{T_{H} - T_{C}}{R} = \frac{4 π K (T_{H} - T_{C}) r_{1} r_{2}}{(r_{2} - r_{1})}$

|

Updated on:21/07/2023

Class 12 PHYSICS HEAT - 1

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two spheres of the same material having radii $r$ and $4 r$ and temperature $2 T_{0}$ and $T_{0}$ respectively. The ratio of rate of radiation of energy by the sphere is
A $1 : 1$
B $1 : 2$
C $2 : 1$
D $3 : 1$
Question 2 - Select One
The figure shows a system of two concentric spheres of radii $r_{1} and r_{2}$ are kept at temperature $T_{1} and T_{2}$ , respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to

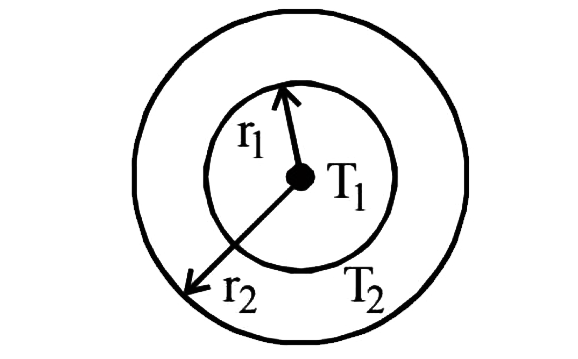A $I n (\frac{r_{2}}{r_{1}})$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}}$
C $(r_{1} - r_{2})$
D $\frac{r_{1} r_{2}}{r_{2} - r_{1}}$
Question 3 - Select One
Space between tow concentric spheres of radii $r_{1} and r_{2}$ such that $r_{1} < r_{2}$ is filled with a material of resistivity $ρ$ . Find the resistance between inner and outer surface of the material

A $\frac{r_{1}}{r_{2}} \frac{p}{2}$
B $\frac{r_{2} - r_{1}}{r_{1} r_{2}} \frac{p}{4 π}$
C $\frac{r_{1} r_{2}}{r_{2} - r_{1}} \frac{p}{4 π}$
Dnone of these.

MOTION-HEAT - 1-EXERCISE -4 (Level - II) Previous Year | JEE Advanced

Home
Ask Doubt
Profile