Electric current is passing uniformly through a solid cylindrical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder $(r < R)$ varies as shown in

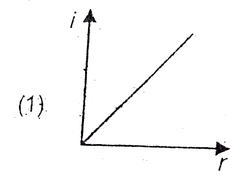
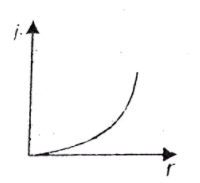
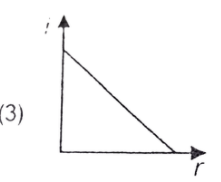
ocr_image

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Electric current is passing uniformly through a solid cylindrical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder $(r < R)$ varies as shown in
A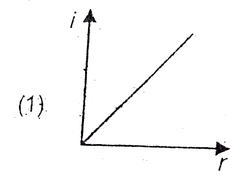
B
C
D
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
A $B = 0$ at the axis
B $B \propto x$ for $0 \leq x \leq r$
C $B \propto 1 / x$ for $x > r$
DB is maximum for $x = r$
The current density varies radical distance r as $J = a r^{2}$ , in a cylindrical wire of radius R. The current passing through the wire between radical distance $R / 3 and R / 2$ is,
A $\frac{65 π a R^{4}}{2592}$
B $\frac{25 π a R^{4}}{72}$
C $\frac{65 π a^{2} R^{3}}{2938}$
DNone of these