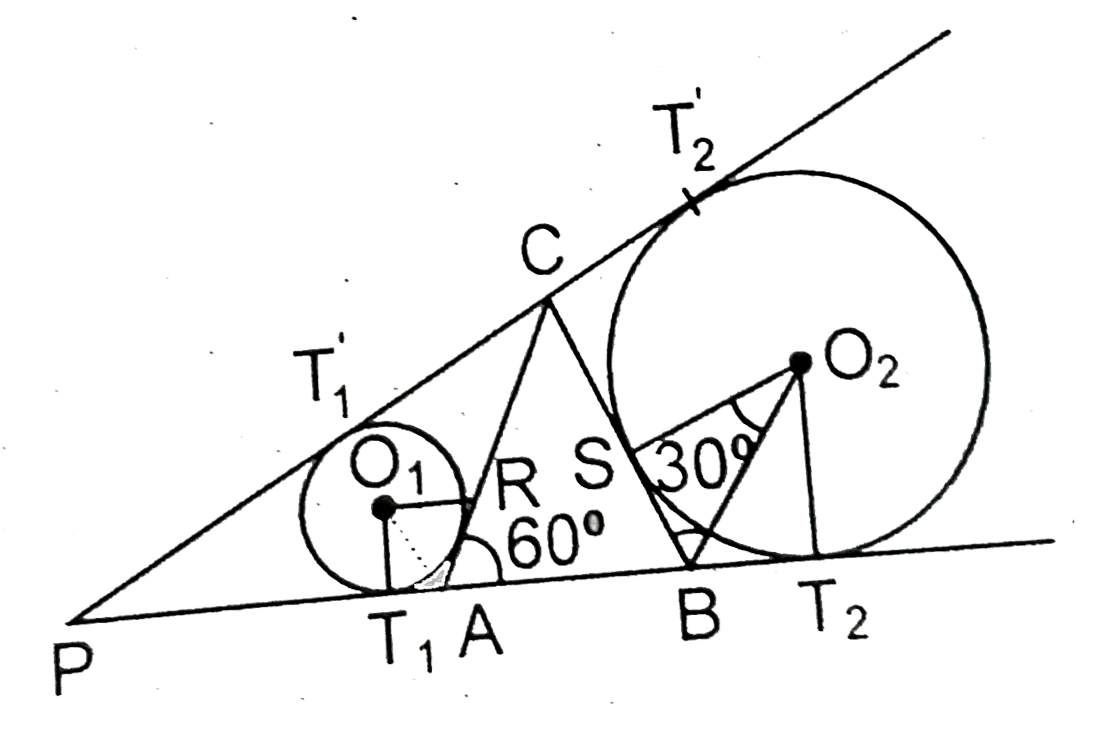
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
The correct Answer is:00000.50
∠T1O1R=60∘ and ∠AO1R=0∘
similarly ∠BO2S=30∘
T1T2=T1A+AB+BT1=RA+RB+SB
=r1tan30∘+a+r2tan30∘=r1+r2√3+a
and T′1T′2=T′1C+T′2C=a−RA+a−BS=2a−r1+r2√3
Since common external tangents are equal T1T2=T′1T′2
⇒r1+r2=√3a2
Topper's Solved these Questions
Similar Questions
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionIf ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View Solution
Knowledge Check
ABC is an equilateral triangle. P,Q and R are the midpoints of sides AB, BC and CA respectively. If the length of the side of the triangle ABC is 8 cm, then the area of △PQR is:
ABC एक समबाहु त्रिभुज है | P, Q और R क्रमशः भुजाओं AB, BC तथा CA के मध्य बिंदु हैं | यदि त्रिभुज ABC की भुजा की लंबाई 8 सेमी है, तो त्रिभुज PQR का क्षेत्रफल कितना होगा ?A4√3cm2B8√3cm2C√3/3cm2D√3/4cm2The incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
A∣∣∣4Rsin.A2sin.B−C2∣∣∣B∣∣∣4Rcos.A2sin.B−C2∣∣∣C|b−c|D∣∣∣b−c2∣∣∣Consider a triangle ABC and let a, b and c denote the lengths of the sides opposite to vertices A, B and C, respectivelu. Suppose a=6,b=10 and the triangle is 15√3. If ∠ACB is obtus and if r denotes than radius of the incircle of the triangle, then the value of r2 is _____
A√3B2√3C3D4.5
Let the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of equilateral triangle be along the straight line x+y=3. If R and r be the radius of circumcircle and incircle respectively of △ABC, then (R+r) is equal to :
View SolutionLet ABC be an equilateral triangle with side length a. Let R and r denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of a, the ratio Rr
View Solution
If a circle touches the side BC at point P, extended side AB at Q and extended side AC at R. Then AQ is equal to :
View SolutionIn ΔABC ,with usual notations r1,r2,r3 are in harmonic progression. If area of ΔABC is 24 and perimeter is 24 then length of its sides are
View SolutionIn ΔABC,∠B=2∠C. D is a point on side BC such that AD bisects ∠BACandAD=CD. Find the value of ∠BAC.
View Solution