Two identical small elastic conducting balls of mass m and radius r have charges of oppsite signs Q and -q. Inditially they are held in free space with their centres at separation l>2r and then released Their speeds v long after their collision is
v=
⎷1a×πε0m{(Q+q)2b×r−Qql}
(Ignore non-uniformity in charge distributuion when ball come close to each other, magnetic field produced by motion of charges and the gravitational interaction between them). Find (6×a×b×48? (a and b are lowest possible integers)
The correct Answer is:4
v=
⎷14πε0m{(Q+q)28r−Qq1}
kinetic energies of the ball can only change due to work done by interaction forces. The loss of energy due to redistribution of charge between the balls at time of contact will dissipate as heat and nothing to do with change in kinetic energy. Therefore, the balls gain kinetic energy at the expense of interaction energy before the collision, during collision they exchange their velcities and after the collision, they further gain kinetic energy at the expense of their interaction energy.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic48videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Two identical conducting balls A and B have charges- Q and + 3Q respectively. They are brought in contact with each other and then separated by a distance d part. Find the nature of the Coulomb force between them.
View SolutionTwo identical conducting balls A and B have charges -Q and +3Q respectively . They are brought in contact with each other and then separated by a distance d apart. Find the nature of the coulumb force between them.
View Solution
Knowledge Check
- Question 1 - Select One
Two metallic spehres each of mass M and radius R charged separately to Q1 and Q2 are at a distance d between their centres (d>2R) The force between them will be
A14πε0Q1Q2d2B> 14πε0Q1Q2d2C< 14πε0Q1Q2d2Dzero - Question 2 - Select One
Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1 - Question 3 - Select One
Charge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
Aμ0qvrBμ0qvrCμ0vqrDμ0qvr
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance from each other. What is the speed of each charged particle when they are at a distance 2r ?
View SolutionMetallic sphere of radius R is charged to potential V. Then charge q is proportional to
View SolutionTwo similar conducting balls having charges + q and - q are placed at a separation d from each other in air. The radius of each ball is r and the separation between their centres is d (d >> r ). Calculate the capacitance of the two ball system
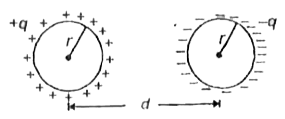 View Solution
View SolutionA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q(R>r0. The potential difference between the two is
View Solution

