A long thin pliable carpet is laid on the floor. One end of the carpet is bent back and then pulled backwards with constant unit velocity just above the part of the carpet which is still at rest on the floor. Speed of centre of mass of the moving part is (2×xmm)/sec. Then find x75?

The correct Answer is:5
Condinates of centre of mass after time t is
xCM=3x4
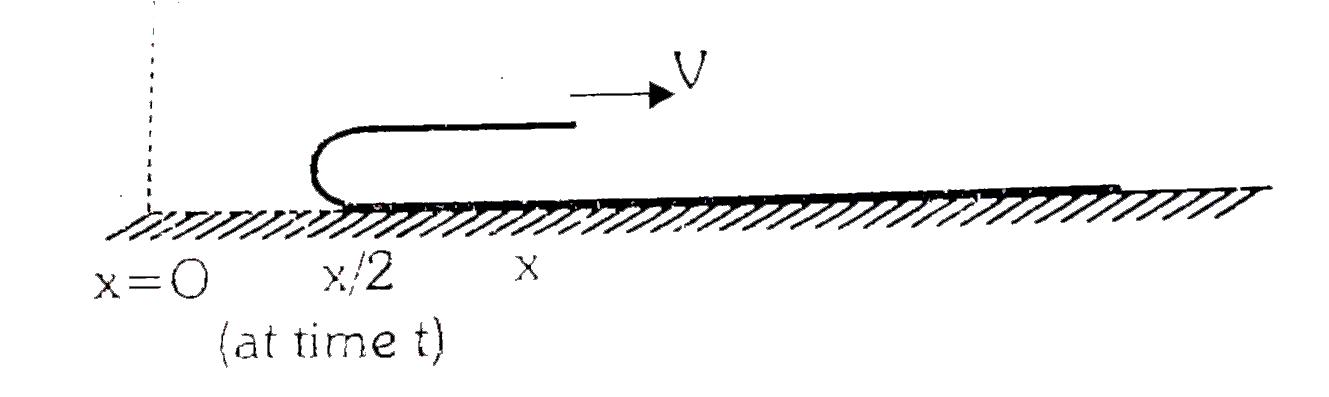
VCM=dxCMdt=34dxdt....(i)
dxdt=V.....(ii)
VCM=34V=34m/sec=750mm/sec
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic48videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS45videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
A carpet of unit mass an unit length is laid on the floor. One end of the carpet is bent back and then pulled backwards with constants. Unit velocity, just above the part of the carpet which is still at rest on the floor. Find the speed of the centre of mass of the moving part. What is the minimum force needed to pull the moving part ?
 View Solution
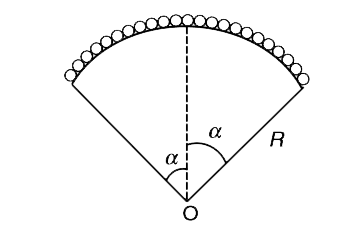
View Solution(a) A uniform chain is lying in form of on arc of a circle of radius R. The arc subtends an angle of 2α at the centre of the circle. Find the distance of the centre of mass of the chain from the centre of the circle.
(b) A uniform chain of length πR2 is lying symmetrically on the top of a fixed smooth half cylinder (see figure) of radius R. The chain is pulled slightly from one side and released. It begins to slide. Find the speed of the chain when its one end just touches the floor. What is speed of centre of mass of the chain at this instant ?
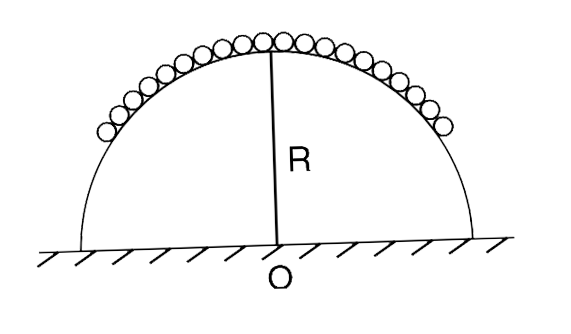
(c) In part (b) assume that the half cylinder is not fixed and can slide on the smooth floor. Find the displacement of the cylinder by the time one end of the chain touches the floor. Mass of cylinder is equal to that of the chain. For part (b) and (c) assume that the chain remains in contact with the cylinder all the while.View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
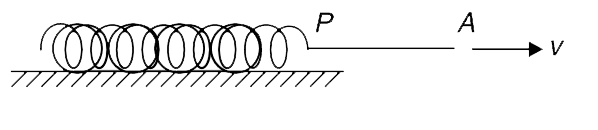
View SolutionA heap of rope is lying on a horizontal surface. One free end A of the rope is pulled horizontally with a constant velocity v. Assume that the heap does not move and the moving part of the rope remains straight and horizontal (i.e. there is no sag). Mass per unit length of the rope is λ. Find the tension at point P where the straightened part of the rope meets the heap. How much force the external agent must apply at end A ?
 View Solution
View SolutionA block of mass 25kg rests on a horizontal floor (μ=0.2). It is attached by a 5m long horizontal rope to a peg fixed on floor. The block is pushed along the ground with an initial velocity of 10m/s so that it moves in a circle around the peg. Find
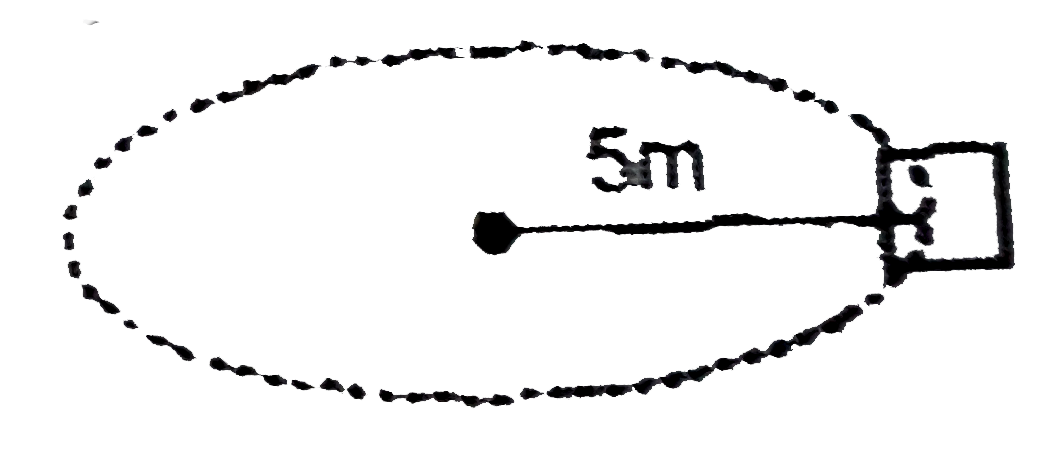
(a) Tangential acceleration of the block.
(b) Speed of the block at time t.
(c) Time when tension in rope becomes zero.View SolutionA boy of mass 40kg moves on a 10m long , 60kg railroad car on the smooth horizontal floor. Now the boy moves with speed 5m/s. (a) Find the velocity of the car with respect to the floor. (b) If the boy starts from middle of the car and reaches to one end of the car , find the distance traveled by the car. (c ) If the boy stops at the end , find the velocity of the car. (d) If the boy falls off the car at one end while walking , find the velocity of the car.
View SolutionA thin carpet of mass 2m is rolled over a hollow cylinder of mass m. The cylinder wall is thin and radius of the cylinder is R. The carpet rolled over it has outer radius 2R (see figure). This roll is placed on a rough horizontal surface and given gentle push so that the carpet begins to roll and unwind. Friction is large enough to prevent any slipping of the carpet on the floor. Also assume that the carpet does not slip on the surface of the cylinder. The entire carpet is laid out on the floor and the hollow cylinder rolls out with speed V. Find V.
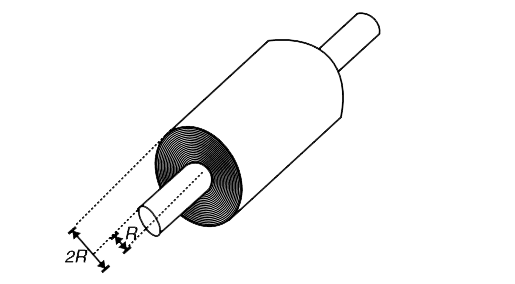 View Solution
View Solution(i) A footpath of uniform width runs all around the inside of a rectangular field 54 m long and 35 m wide . If the area of the path is 420 m2, find the width of the path .
(ii) A carpet is laid on the floor of a room 8m by 5m , there is a border of constant width all around the carpet . If the area of the border is 12m2 , find its width .View SolutionA very flexible chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest intantaneously find the force exerted by the floor of the lift on the chain at the moment when one fourth of the chain has already landed on the floor Assume the lift is moving with acceleration g/2
View SolutionAB is a long frictionless horizontal surface. One end of an ideal spring of spring constant K is attached to a block of mass m, which is being moved left with constant velocity v, and the another end is free. Another block of mass 2m is given a velocity 3v towards the spring. Magnitude of work done by external agent in moving m with constant velocity v in long time is β times mv2 . Find the value of β
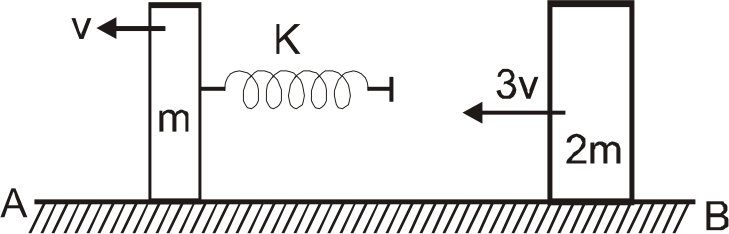 View Solution
View Solution

