Construct a quadrilateral ABCD
in which AB=4.4 cm, BC=4cm, CD=6.4cm, DA=3.8cm and BD=6.6cm.
Steps for construction:
Step 1: Draw a line segment BC = 4cm
Step 2: Draw an arc of 6.4cm from point C and an arc of length6.6cm from pointBwhich cuts one another at pointD
Step 3: Join the point D toB and D to C.
Step 4: Again draw an arc of 3.8 cm. from pointD and an arc of length4.4cm from pointB which cuts one another at point A Step 5: Join the point A to B and A to D.
Step 6: Thus ABCD is the required quadrilateral.
Topper's Solved these Questions
Similar Questions
Which of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
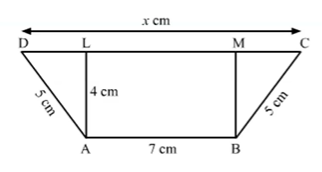
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
 View Solution
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionCalculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionIn ABC and DEF , it is being given that: AB=5cm, BC=4cm and CA=4.2cm ; DE=10cm , EF=8cm and FD=8.4cm . If AL⊥BC and DM⊥EF , find AL:DM .
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
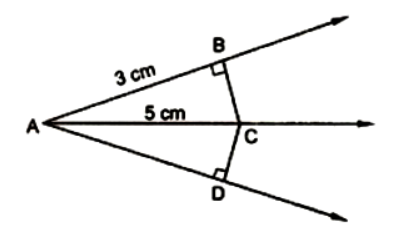
View SolutionIn Figure, if AC is bisector fo ∠BAD such that AB=3 cm and AC=5 cm, then CD= 2 cm (b) 3 cm (c) 4 cm (d) 5 cm
 View Solution
View Solution

