Trajectory of a particle in a projectile motion is given by y=x−x280 where x and y are in meters. Match the column-1 and column-2.
Column-IColumn-II(A)x coordinate at height of 15 m(P) 20 m(B)vertical distnce of particle frompoint of projection at x= 100 m(Q) 80 m(C)Horizontal range(R) 60 m(S) 25 m
The correct Answer is:[(A)PR(B)S(C)Q]
(A)15=x−x280
1200=80x−x2
x2−80x+1200=0
x2−60x−20x+1200=0
x=60,20
(B) y=100−(100)280=100−100082=25
(C) Hzran≥:x−x280=0⇒x(x−x80)=0,x=(0,80)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
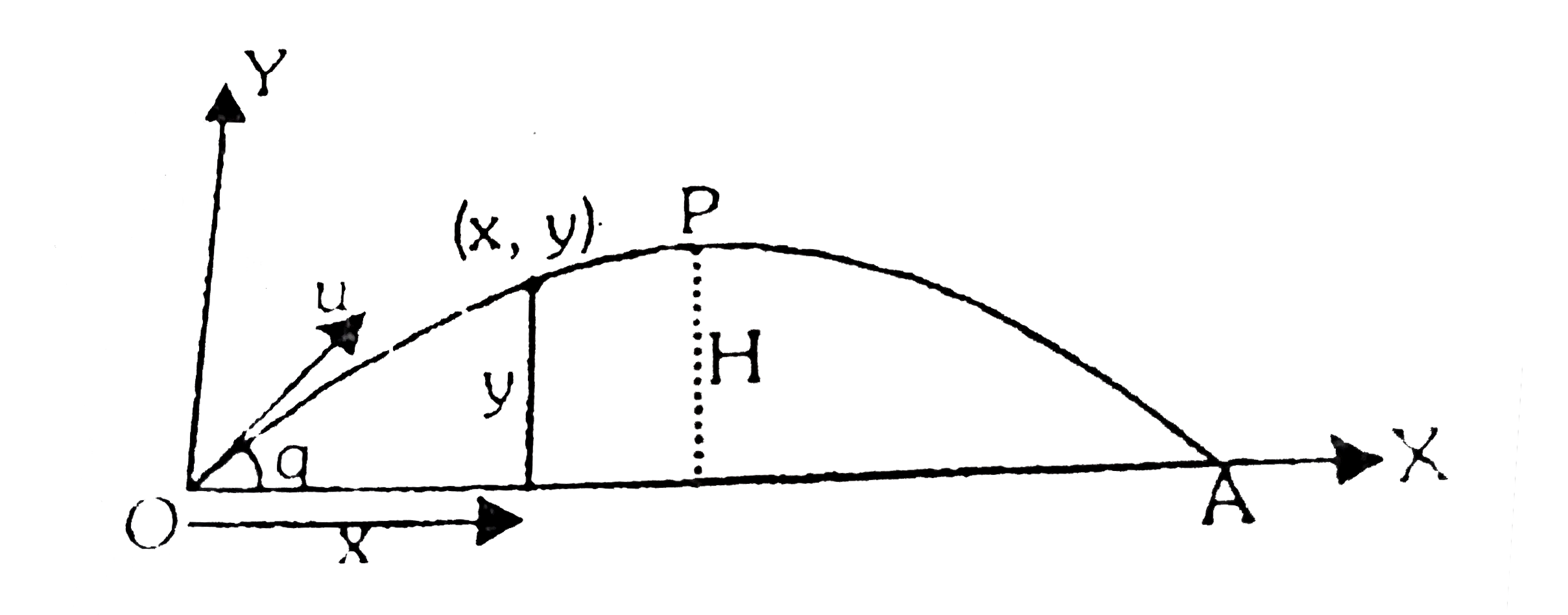
Range OA is :-A√32B√34C√3D38The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Angle of projection θ is :-A30∘B60∘C45∘D√3 radEquation of trajectory of a projectile is given by y=−x2+10x where x and y are in meters and x is along horizontal and y is vericall y upward and particle is projeted from origin. Then : (g=10)m/s2
Ainitial velocity of particle is √505m/sBhorizontal range is 10mCmaximum height is 25mDangle of projection with horizontal is tan−1(5).
Trajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
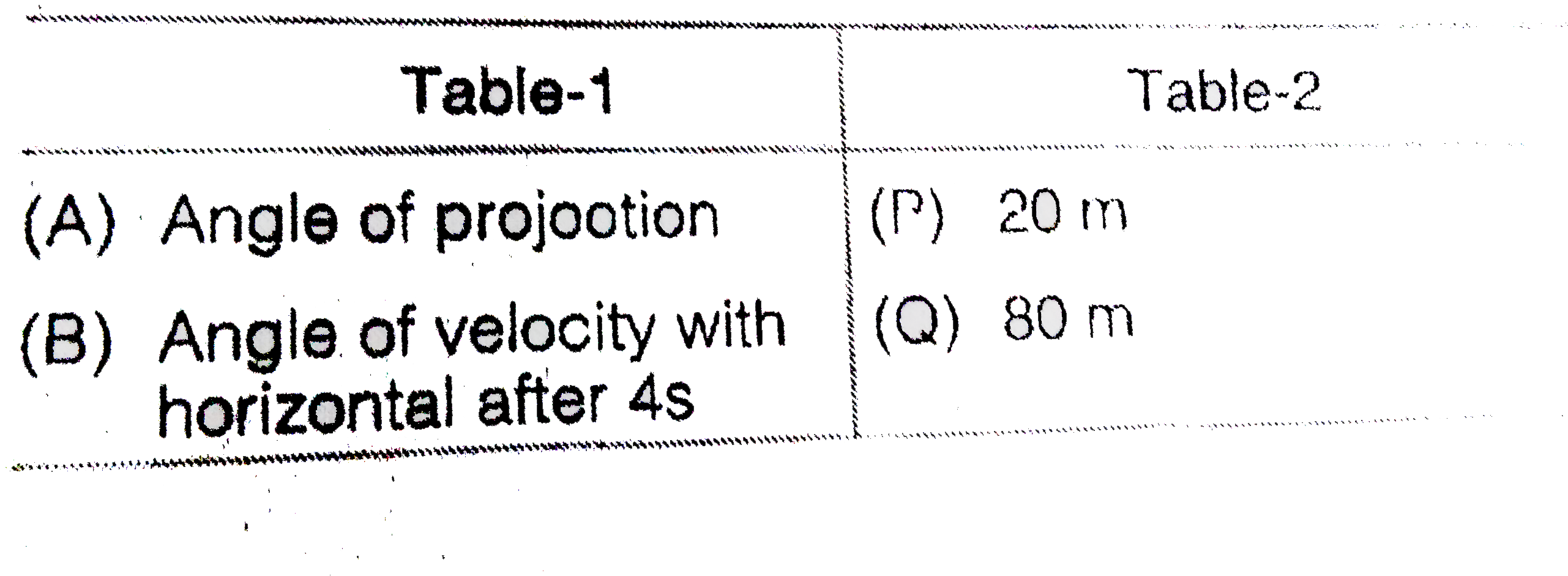
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion match the following with g=10ms−2.

View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Maximum height H is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View Solution


