A block of mass m=1kg is attached to a free end of a spring whose one end is fixed with as shown in the figure. The block is performing simple harmonic motion. The position of the block from O is given by x=2+1√2sin2t, where x is in meter and t is in second. A particle of same mass is released from the circular path at a height h=80cm. then particle collidic and stricks to the block. The collision takes place when velocity of the block is zero and spring is elongated. Find
(i) Time period of new SHM.
(ii) Maximum velocity of the system

x=2+1√2sin2t
⇒2=√km⇒k=4N/m
ωL=1ωC
Just before collision, velocity of the shell,
2ωL=12ωC'
Now , Pi=Pr
0+mx4=(m+m)xv0⇒v0=2m/s
Using conservation of energy,
∴C'=14ω2L=LC4L=C4kx2+∴ΔCC=34(2m)(2)2
=1f1=(1.5−1)R+(43−1)(−1R−1R)+(1.5−1R)=1R−23R=13R(2m)v'2
=1f2=(1.5−1)R+(43−1)(−1R)+(1.5−1R)=1R−13R=23R

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
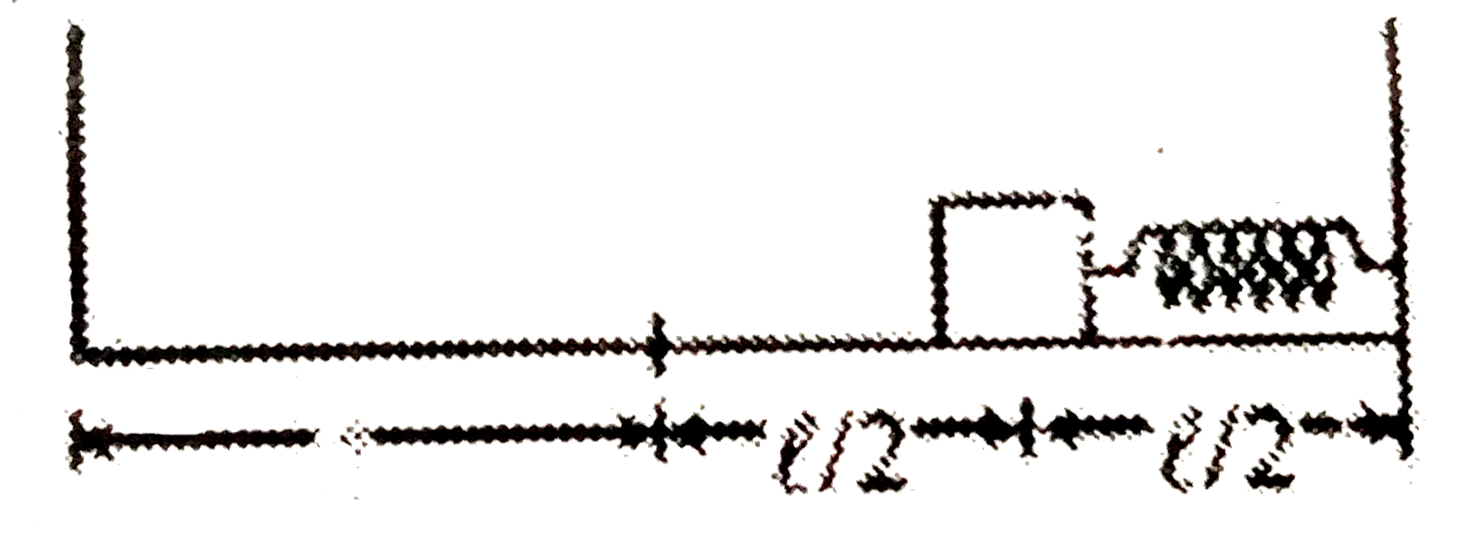
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
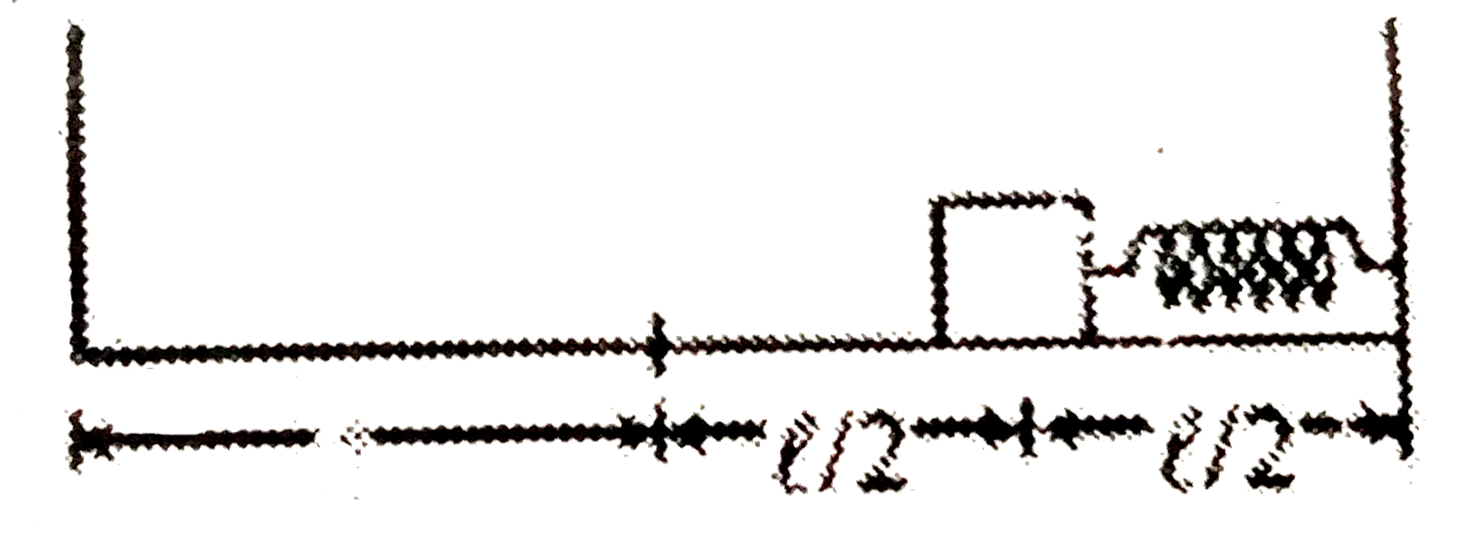 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of theseA block of mass 1 kg is pushed towards another block of mass 2 kg from a 6 m distance as shown in the figure. If just after the collision, the velocity of 2 kg block is 4ms−1, then
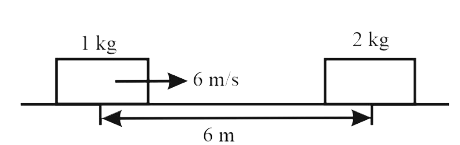 ACoefficient of restitution between the blocks is 1BCoefficient of restitution between two blocks is 1/2CCoefficient of restitution between two blocks is 1/3DCoefficient of restitution between two blocks is 1/4
ACoefficient of restitution between the blocks is 1BCoefficient of restitution between two blocks is 1/2CCoefficient of restitution between two blocks is 1/3DCoefficient of restitution between two blocks is 1/4A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
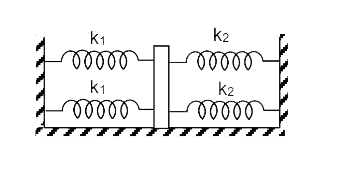 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :

View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View Solution
