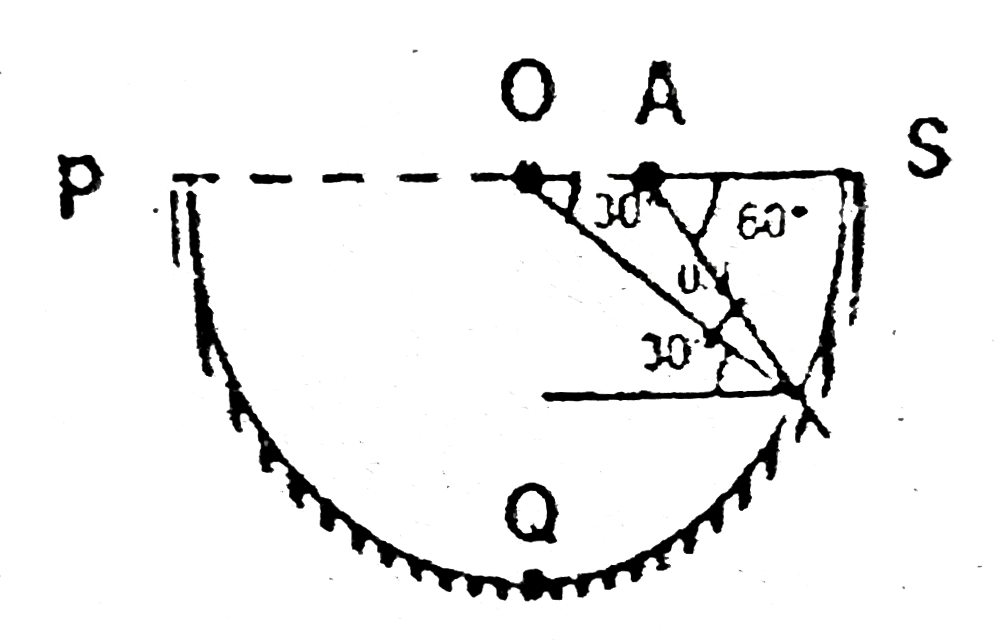
A ball is thrown from point A making an angle 60∘ with line OAS as shown in the figure, where OA=R√3 [O is the centre of spherical surface of PQS]. If after striking the hemi-spherical surface, the ball rebounds in direction parallel to OA. The coefficient of restitution between the ball and the surface is [Neglect the effect of gravity any type of frictional force]
![A ball is thrown from point A making an angle 60^(@) with line OAS as shown in the figure, where OA=(R )/(sqrt(3)) [O is the centre of spherical surface of PQS]. If after striking the hemi-spherical surface, the ball rebounds in direction parallel to OA. The coefficient of restitution between the ball and the surface is [Neglect the effect of gravity any type of frictional force]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PHY_GMP_ASS_E01_278_Q01.png)
e=0.50
e=0.75
e=0.25
None of these
Rsin120∘=R/√3sinθ
⇒sinθ=1/2⇒θ=30∘
Hence e=1
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A ball is dropped from a heght of 3.6 m and strikes a horizontal surface . It rebounds from the horizontal surface to height h . Calculate h , if coefficient of restitution is 0.6
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View Solution
Knowledge Check
A ball is dropped on a horizontal surface from height h. If it rebounds upto h2 after first collision then coefficient of restitution between ball and surface is
A1√2B12C14D12+√2A ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
A1√2B12C14D12√2A particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
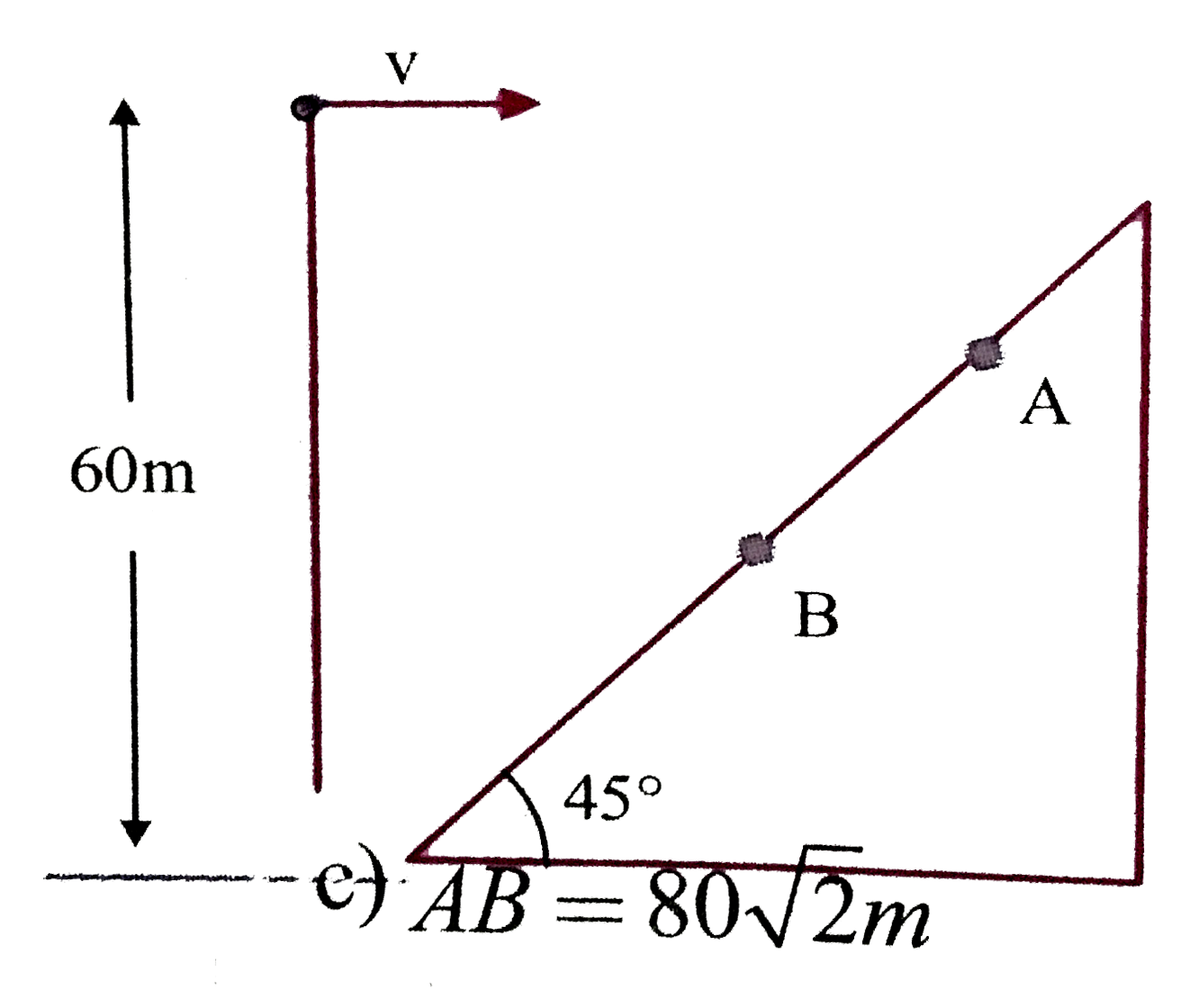 Av=20m/sBv=10m/sCAB=80√2mDAB=80m
Av=20m/sBv=10m/sCAB=80√2mDAB=80m
A ball is thrown from a point O with a velocity u=20ms−1 at an angle θ=30∘ with the horizontal.It hits a vertical wall which is at a distance x , from O as shown in the figure.After rebounding from the wall, the ball returns to O without retracing its path. If g=10ms−2 and the coefficient restitution e=0.5 ,the value of x is
View SolutionA ball is thrown from a point at a distance c from a smooth vertical wall and after striking against the wall it returns to the point of projection. Take 'e' to be the coefficient of restitution between the ball and the wall. If α be the angle of projection with the horizontal and u the velocity of projection, then
u= ⎷{(1+e)gcesin2α} and time of flight
T= ⎷{2(1+e)ctanαeg}
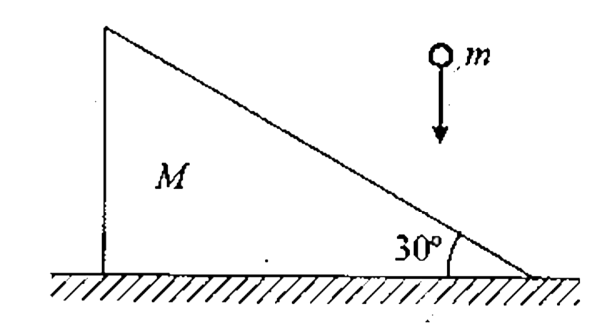
View SolutionA ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
View SolutionA staircase has each step of height h and width x. A ball strikes the centre point of a step with velocity v making an angle θ with the vertical. It rebounds and strikes the centre point of the next step. Once again it rebounds and hits the centre point of the next step and so on.

Assume that there is no friction between the ball and the steps and coefficient of restitution is e.
(a) Show that each time after hitting a step, the ball climbs to the same height (i.e., heights like AB and CD shown in figure are equal).
(b) Find h and x.
View SolutionA ball is vertically downward with speed 5√2 m/s to hit a horizontal surface as shown in the figure. The coefficient of resitution for the collision is 12 and friction coefficient 1√3. Calculate the speed (m/s) of the ball just after the collision.

View Solution
