A triangular of rigid wire frame 'AOB' is made, in which length of each wire is l and mass m. The whole system is suspended from point O and free to perform SHM about x-axis or about z−axis. When it performs SHM about x−axis its time period of oscillation is T1 and when it performs SHM about z−axis, its time-period of osciallation is T2, then choose the correct option.
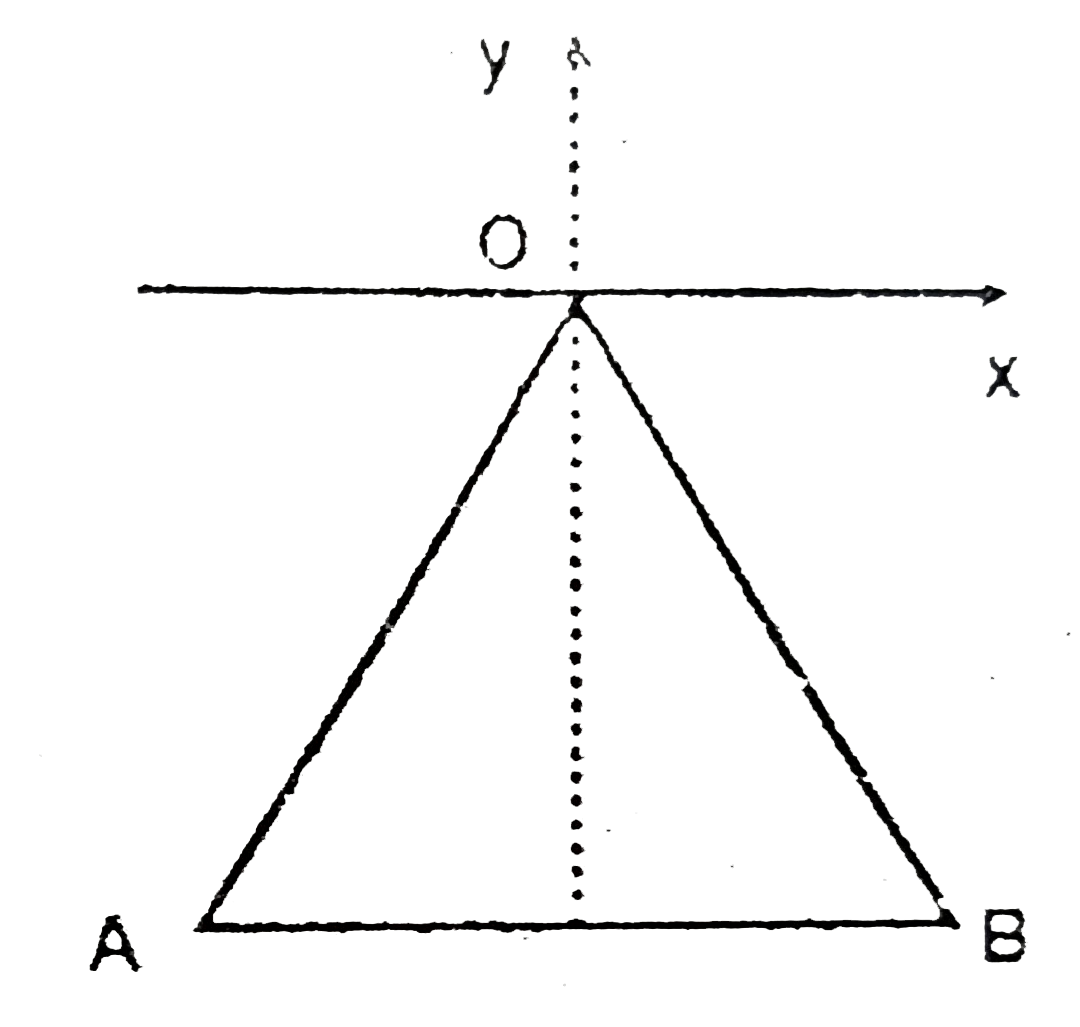
T1<T2
T1>T2
T1=T2
None
T=2π√1Msysgd, Msys=3m, d=l√32×23=l√3
Case I : System is performing SHM about x−axis
IX=IAB+IAO+IBO=3ml24+[ml23sin260∘]×2=5ml24
T1=2π√IxMsysgd=2π
⎷5ml24×√33m×g×l=2π√5√3l12g
Case II : System is performing SHM about z− axis
Iz=IAB+IAO+IBO=⎡⎣ml212+m(√3l2)2⎤⎦+ml23+ml23=ml2[112+34+23]
=ml2[1+9+812]=3ml22
T2=2π√IzMsysgd=2π√3ml2×√32×3m×g×l=2π√√3l2g
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A particle is performing SHM aong x-axis,such that its velocity is v1 when its displacement from mean position is x1 and v2 when its displacement from mean position is x2.Time period of oscillation is
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
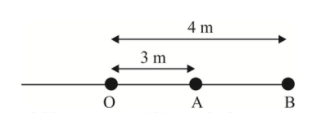 A0.18 sB0.20sC0.15sD0.24s
A0.18 sB0.20sC0.15sD0.24sA particle performing SHM is found at its equilibrium position at t = 1s and it is found to have a speed 0.25 = m//s at t=2s. If the period of oscillation is 6. Calculate amplitude of oscillation.
A32πmB34πmC6πmD38πm
A thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View SolutionAn object performs S.H.M. of amplitude 5 cm. and time period 4 sec. If timing is started when the object is at the centre of the oscillation i.e., x = 0 then calculate.
(i) Frequency of oscillation
View SolutionA particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
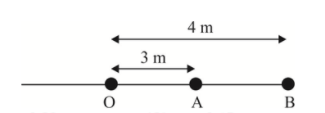
View SolutionA particle performing SHM is found at its equilibrium position at t = 1s and it is found to have a speed 0.25 = m//s at t=2s. If the period of oscillation is 6. Calculate amplitude of oscillation.
View SolutionA simple pendulum performs SHM about x=0 an amplitude a and time period T. the speed of pendulum at x=a2 will be
View Solution
