The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such casesdinKdT=EaRT2 should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
If for a reaction in K=20−20T+3 in T then Ea at 300 K will be
20 R
900 R
920 R
880 R
The correct Answer is:C
Step by step video, text & image solution for The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such cases(d"in"K)/(dT)=(E_(a))/(RT^(2)) should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow : If for a reaction in K=20-(20)/(T)+3 in T then E_(a) at 300 K will be by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 21videos
GRAPHICAL INTERPRETATION
- BOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 31videos
GRAPHICAL INTERPRETATION
- BOOK - GRB PUBLICATIONCHAPTER - GRAPHICAL INTERPRETATIONEXERCISE - Comprehension 11videos
GRAPHICAL INTERPRETATION
- BOOK - GRB PUBLICATIONCHAPTER - F-BLOCK ELEMENTSEXERCISE - Subjective type7videos
F-BLOCK ELEMENTS
- BOOK - GRB PUBLICATIONCHAPTER - HYDROCARBON (ALIPHATIC)EXERCISE - Previous years jee questions28videos
HYDROCARBON (ALIPHATIC)
Similar Questions
Which one of the following given graphs represents the variation of rate constant (k) with temperature (t) for an endothermic reaction ?
View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
View Solution
Knowledge Check
- Question 1 - Select One
The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such casesdinKdT=EaRT2 should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
Which if the following statement is not correct ?ATemperature coefficient of a reaction at high temperature will be lessBReaction with no activation energy will have no change in rate constant due to temperatureCThe factor by which catalyst increase rate constant will be same at all the temperatureDGreater the activation energy, more sanitive will the rate constant be cecause of temperature - Question 2 - Select One
The variation of rate constant with temperature can be explained by Arrhenius equation. However , the can be explained by Activation energy is found to be temperature dependent/In such cases dinKdT=EaRT2 should be used to predict variation of rate constant with tempreature. On the basic of this information , answer the question that follow :
If Arrhenius constant and Ea (activation energy0 are assumed to be constant then which of the following graph will be correctA B
B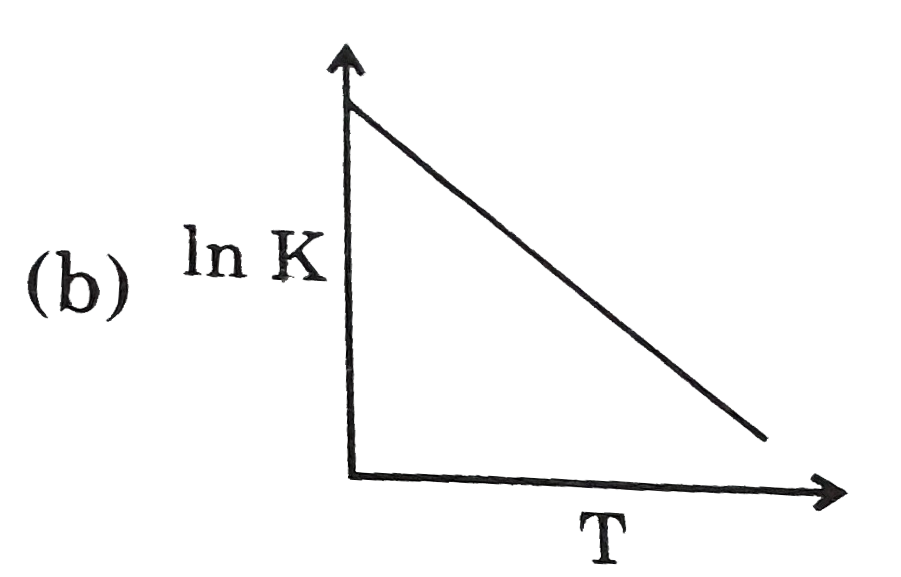 C
C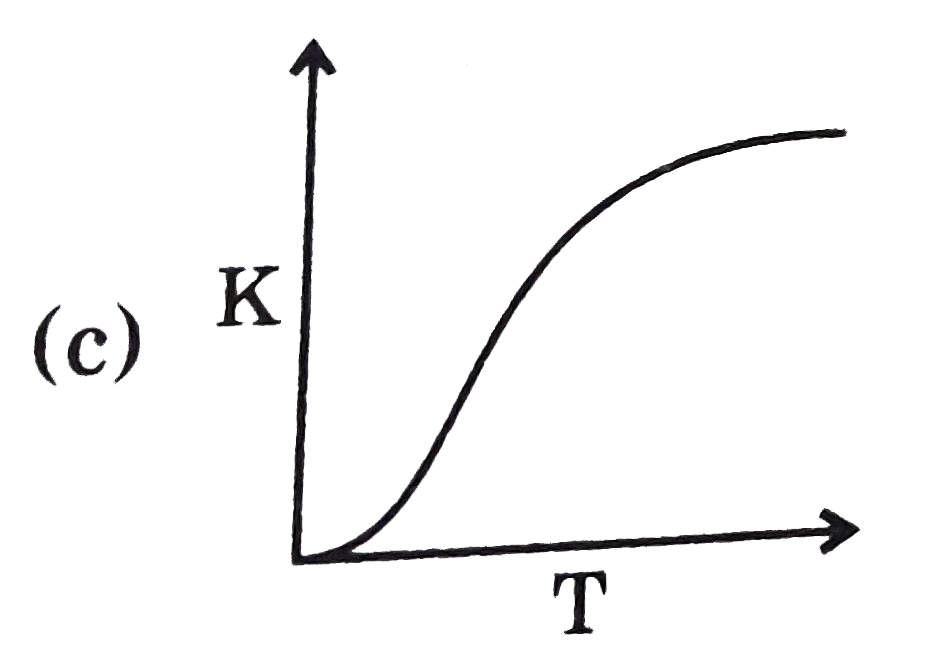 D
D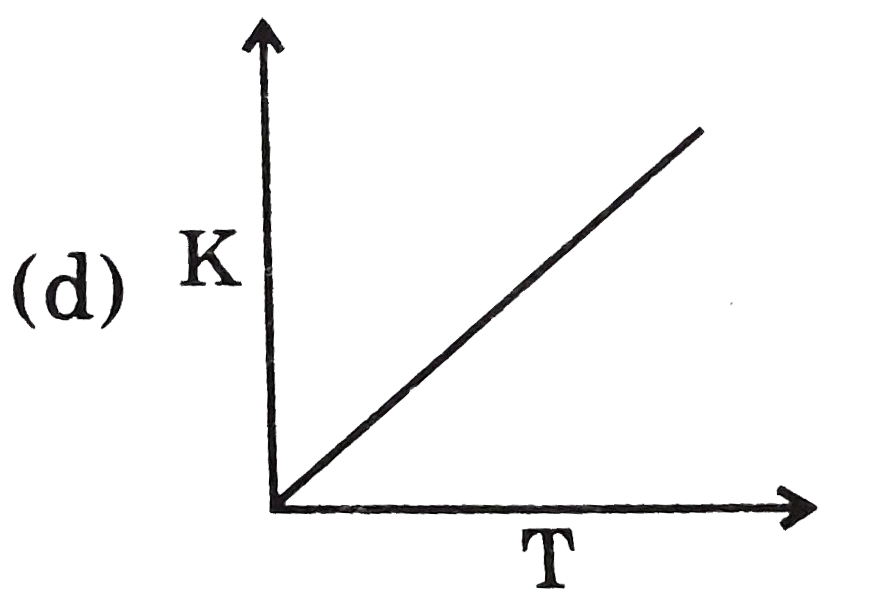
- Question 3 - Select One
Plots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
A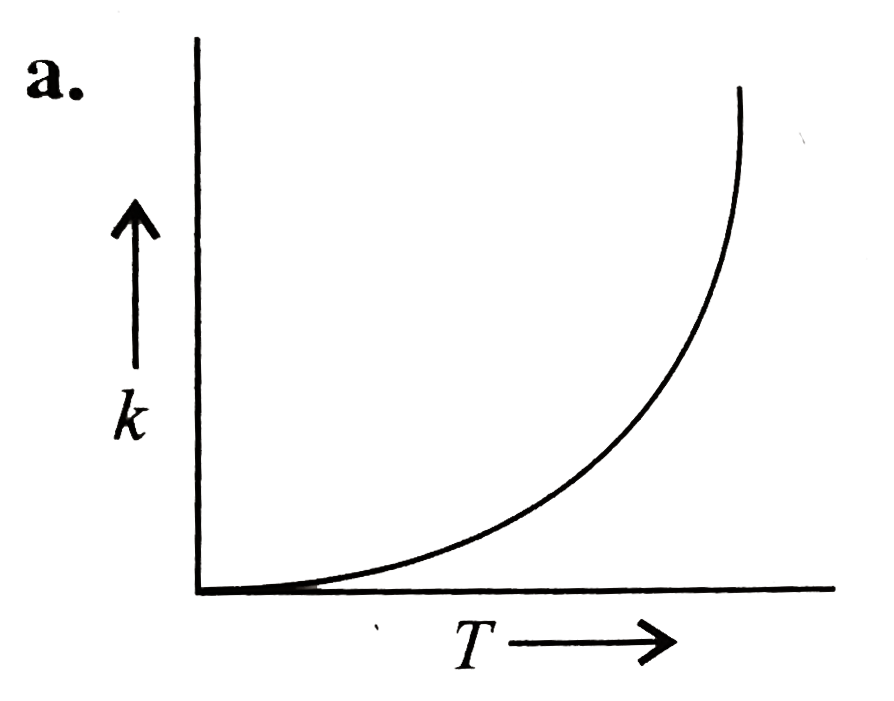 B
B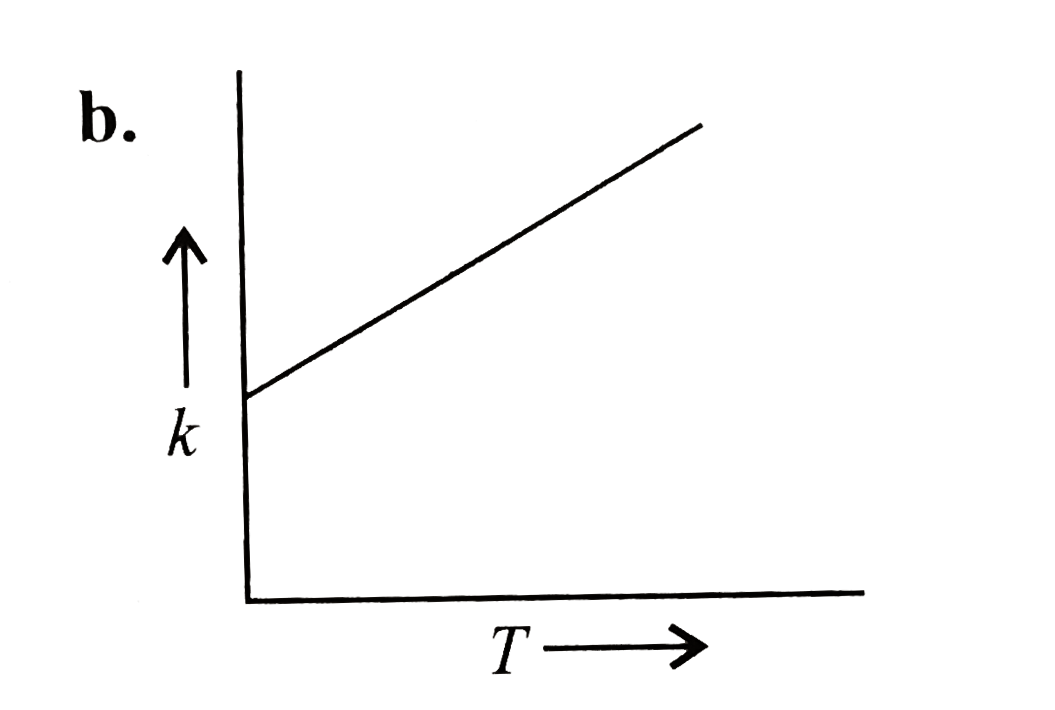 C
C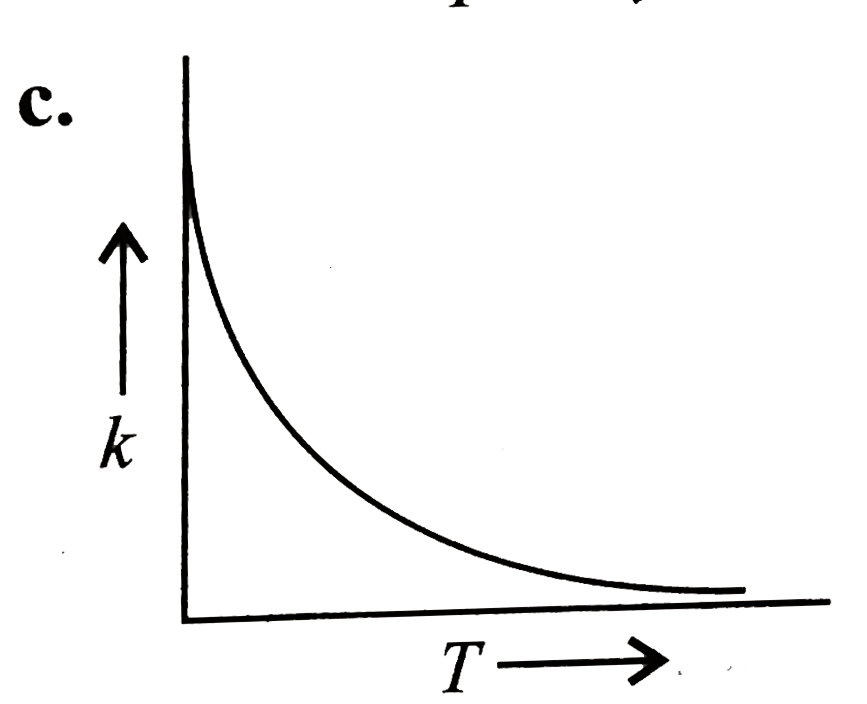 D
D
Arrhenius equation k=Ae−Ea/RT
If the activation energy of the reaction is found to be equal to RT then,View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows Arrhenius equations is
View SolutionWhich of the following graph is incorrect for variation of rate constant (K) with temperature for a reaction obeying Arrhenius equation ?
View SolutionThe variation of rate constant with temperature forllow sthe equations ln k=30−40T+20T2−30lnT based on the this information, indetify the most appropriate option.
View Solution

