In the figure , mass of a ball is 95 times mass of the rod, Length of rod is 1m.The level of ball is same as rod level.Find out time taken by the ball to reach at upper end of rod.

1.4s
2.45s
3.25 s
5 s
The correct Answer is:A
Step by step video, text & image solution for In the figure , mass of a ball is 9/5 times mass of the rod, Length of rod is 1m.The level of ball is same as rod level.Find out time taken by the ball to reach at upper end of rod. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)22videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions14videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
Similar Questions
In the arrangement shown in figure the mass of the ball is η times as that of the rod. The length of the rod is L the masses of the pulleys and the threats as well as the friction, are negligible. The ball is set on the same level as the lower and of the rod and then released. How soon will the ball be opposite the upper and of the rod?
 View Solution
View Solution
if a mass of ball is m/2 and that of a rod is m the length of the rod is 20 cm the ball is set on the same level as the lower end of the rod and then released. If pulleys and strings are light, friction negligible how soon will the ball be opposite top the upper end of the rod?View Solution
Knowledge Check
- Question 1 - Select One
The length of a rod is 5×102 m , the order of magnitude of the length of the rod is
A103mB102mC101mD10−1m - Question 2 - Select One
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpml - Question 3 - Select One
A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
A2[√2gl]B√2glC2[√gl]D√gl
In the arrangement shown in fig the mass of the ball 1 is η=1.8 times as great as that of rod 2 The length of the later is l=100 cm The masses of the pulleys and the threads as well as the friction are negligible The ball is set on the same level as the lower end of the rod and then released How soon will the ball be opposite to the other end of the rod
 View Solution
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
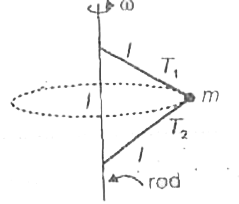 View Solution
View SolutionTwo balls of mass m and 4m are connected by a rod of length L. The mass of the rod is small and can be treated as zero . The size of the balls also can of the neglected . We also assume the centre of the rod is hinged ,but the rod can rotate about its centre in the vertical plane without friction . What is the gravity - induced angular acceleration of the rod when the angle between the rod and the vertical is θ as shown ?
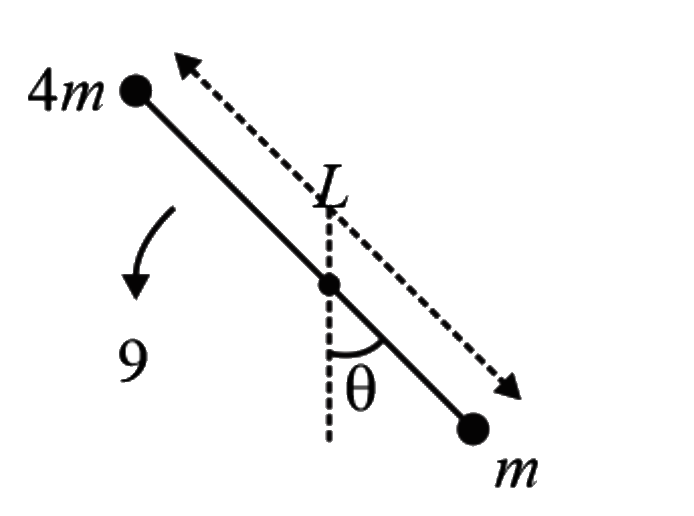 View Solution
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
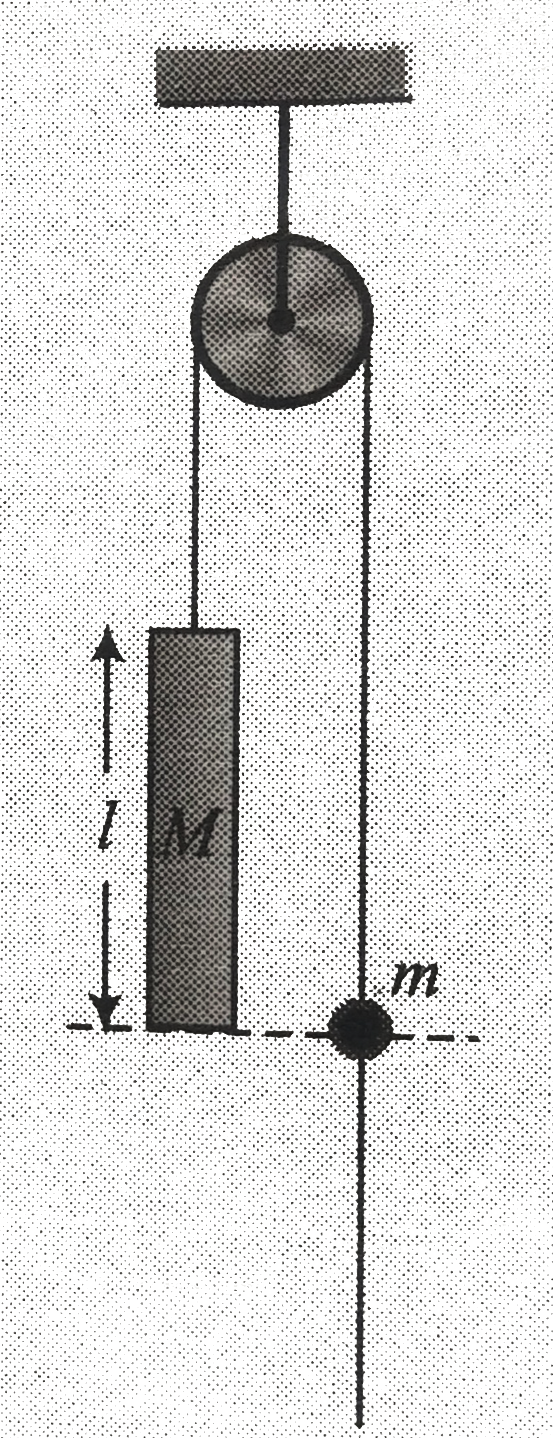 View Solution
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.
 View Solution
View Solution

