Three particle each of mass $m$ , are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?

A

$\sqrt{\frac{G m}{a}}$

B

$\sqrt{\frac{2 G m}{a}}$

C

$\sqrt{\frac{3 G m}{a}}$

D

$\sqrt{\frac{4 G m}{a}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

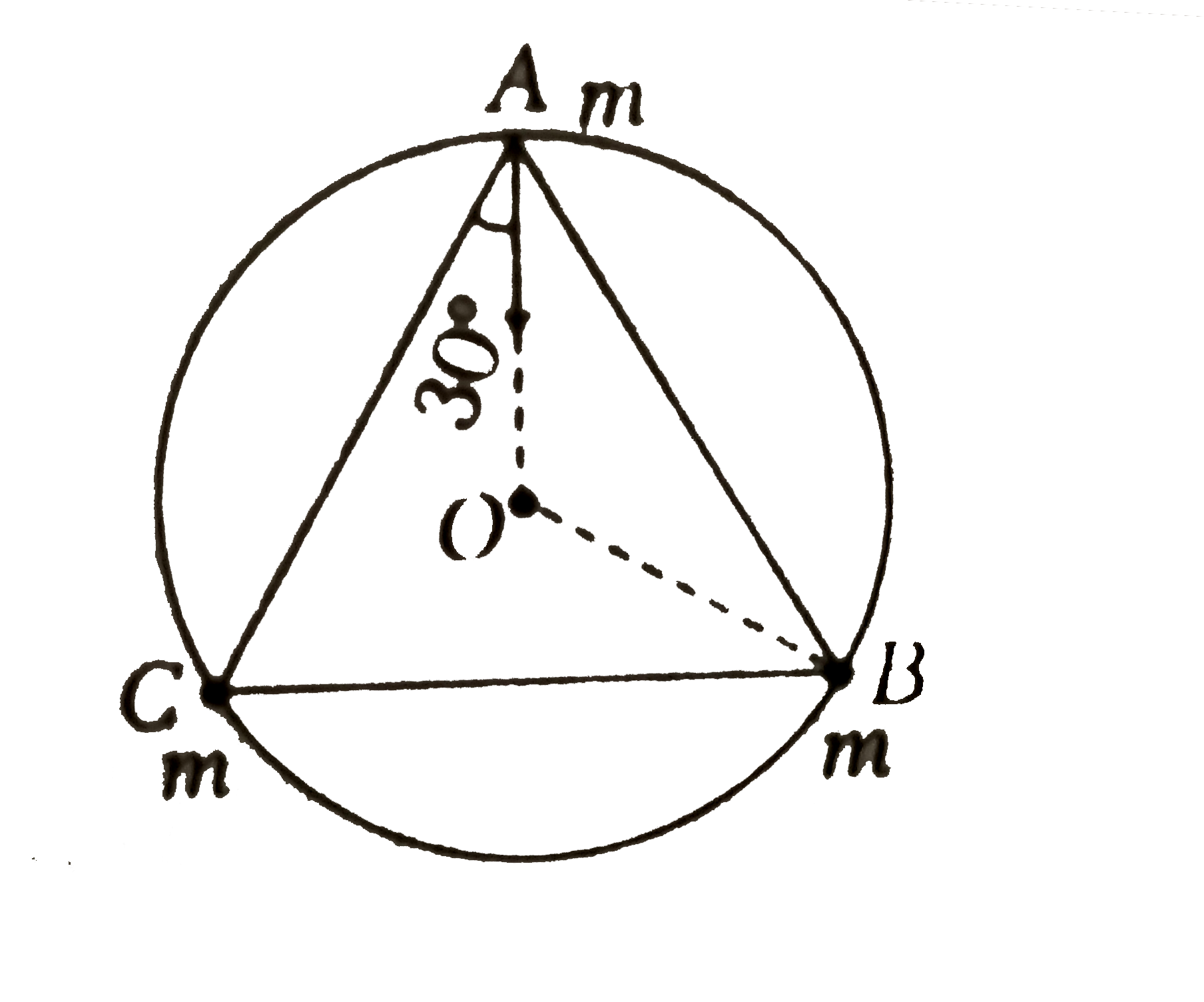
From the figure,
$F_{A} = F_{A B} + F_{A C} = 2 [\frac{G M^{2}}{a^{2}}] {cos 30}^{\circ} = [\frac{G m^{2}}{a^{2}}, \sqrt{3}]$
Also, $r = \frac{a}{\sqrt{3}}$ ,
Now, $\frac{m v^{2}}{r} = F | F_{A} | or \frac{m v^{2} \sqrt{3}}{a} = \frac{G m}{a} = \frac{G m}{a^{2}} \sqrt{3}$
$v = \sqrt{\frac{G m}{a}}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three particles each of mass $m$ are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
Azero
B $\frac{3 G M}{L^{2}}$
C $\frac{9 G M}{L^{2}}$
D $\frac{12 G M}{\sqrt{3} L^{2}}$
Question 2 - Select One
Three indentical bodes of mass M are locatd at the verticles of an equailateral triangle of side L they revolve undr the effect of mutual gravitational force in a circular orbit circumscibing the traingle while preserving the equilateral triangle their orbital velocity is
A $\frac{\sqrt{G M}}{L}$
B $\sqrt{3 G M} / (2 L)$
C $\frac{\sqrt{3 G M}}{L}$
D $\frac{\sqrt{2 G M}}{3 L}$
Question 3 - Select One
Three particles each of mass $m$ are kept at the vertices of an euilateral triangle of side $L$ . The gravitational field at the centre due to these particle is
A $- \frac{3 G M}{L}$
B $- \frac{\sqrt{3} G M}{L}$
C $- \frac{3 \sqrt{3} G M}{L}$
D $- \frac{G M}{3 \sqrt{3} L}$

DC PANDEY-GRAVITATION-(A) Chapter Exercises

Home
Ask Doubt
Profile