Given , ε−Ldidt=iR, find the value of i at any time t in terms of constant ε, L and R. At t=0 , i=0 .
We have , ε−Ldidt=iR
or (ε−iR)=Ldidt
or di(ε−iR)=dtL ...(i)
Integrating both sides of the equation (i), we get
∫di(ε−iR)=∫dtL
Here limit of time varies from 0 to t and corresponding limits of i varies from 0 to i.
∴∫i0di(ε−iR)=∫t0dtL
For integration of LHS, substitute ε−iR=z
Also ddi(ε−iR)=dzdi
or (0−R)=dzdi
∴di=dz(−R)
and ∫t0di(ε−iR)=∫i0dzl(−R)z
=(1−R)∫i0dzz
=(1−R)|lnz|i0
=(1−R)|ln(ε−iR)|i0
=(1−R){ln(ε−iR)−ln(ε−0)}
=(1−R)ln((ε−iR))ε ...(ii)
and RHS ∫t0dtL=(1L))|t|t0=1L(t−0)
=tL
From equation (i) and (ii) , we have
(−1R)ln(ε−iRε)=tL
or ln(ε−iRε)=−RLt
or (ε−iRε)=e−RtL
or i=εR(1−e−tRL)
Topper's Solved these Questions
Similar Questions
If ∫10et1+tdt=a, then find the value of ∫10et(1+t)2dt in terms of a .
View SolutionA current i0 is flowing through an L−R circuit of time constant t0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
View Solution
Knowledge Check
A current i0 is flowing through an L−R circuit of time constant i0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
At0Bet0Ct0eD(1−1e)t0For xε(0,5π2), definite f(x)=∫x0√tsintdt. Then f has
Alocal maximum at π and local minima at 2πBlocal maximum at π and 2πClocal minimum at π and 2πDlocal minimum at π and local maximum at 2pi
If ∫10et1+tdt=a, then find the value of ∫10et(1+t)2dt in terms of a .
View SolutionThe electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.
View SolutionThe electric curren in a charging R-C circuit is given by i=i0e−tRC when i0, R and C aere constant parameters of the circuit and t is time. Find the rate of change of current at a.t=0,b.t=RCc.t=10RC.
View SolutionFor xε(0,5π2), definite f(x)=∫x0√tsintdt. Then f has
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
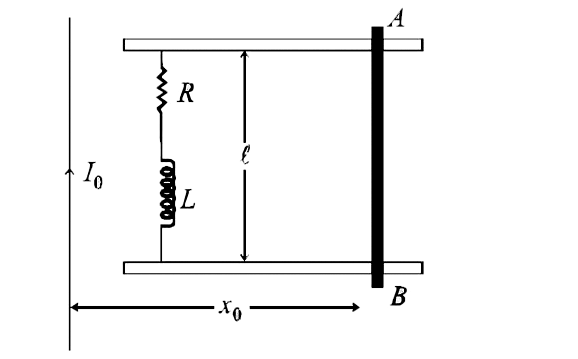
View SolutionA metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.

View Solution
