A current i0 is flowing through an L−R circuit of time constant t0. The source of the current is switched off at time t=0. Let r be the value of (−di/dt) at time t=0.Assuming this rate to be constant, the current will reduce to zero in a time interval of
t0
et0
t0e
(1−1e)t0
The correct Answer is:A
To solve the problem, we need to analyze the behavior of the current in an L-R circuit when the source of current is switched off at time t=0. The current i(t) in the circuit can be described by the following equation:
1. Current Decay Equation:
i(t)=I0e−tτ
where I0 is the initial current, and τ is the time constant of the circuit, given as t0.
2. Differentiating the Current:
To find the rate of change of current, we differentiate i(t) with respect to time t:
didt=−I0τe−tτ
3. Evaluate at t=0:
At t=0, we substitute t=0 into the differentiated equation:
didt∣∣∣t=0=−I0τe0=−I0τ
This value is given as r, thus:
r=−I0τ
4. Finding the Time to Reduce Current to Zero:
We want to find the time tf when the current i(tf) becomes zero. Setting the current equation to zero:
0=I0e−tfτ
Since I0 is not zero, we can ignore it and focus on the exponential term:
e−tfτ=0
However, the exponential function never actually reaches zero. Instead, we can find the time it takes for the current to decay to a negligible amount.
If we assume the current reduces to zero in a time interval that is significant, we can express the time it takes for the current to decay to a very small value (for practical purposes, we can consider it to be when i(t) is approximately 0).
5. Using the Relation Between r and τ:
From the earlier relation r=−I0τ, we can express τ in terms of I0 and r:
τ=−I0r
6. Final Time Calculation:
The time taken for the current to reduce to zero can be approximated as:
tf=τ=I0r
Thus, the time interval required for the current to reduce to zero is:
t0
i(t)=I0e−tτ
where I0 is the initial current, and τ is the time constant of the circuit, given as t0.
To find the rate of change of current, we differentiate i(t) with respect to time t:
didt=−I0τe−tτ
At t=0, we substitute t=0 into the differentiated equation:
didt∣∣∣t=0=−I0τe0=−I0τ
This value is given as r, thus:
r=−I0τ
We want to find the time tf when the current i(tf) becomes zero. Setting the current equation to zero:
0=I0e−tfτ
Since I0 is not zero, we can ignore it and focus on the exponential term:
e−tfτ=0
However, the exponential function never actually reaches zero. Instead, we can find the time it takes for the current to decay to a negligible amount.
From the earlier relation r=−I0τ, we can express τ in terms of I0 and r:
τ=−I0r
The time taken for the current to reduce to zero can be approximated as:
tf=τ=I0r
t0
Similar Questions
During current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t

View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
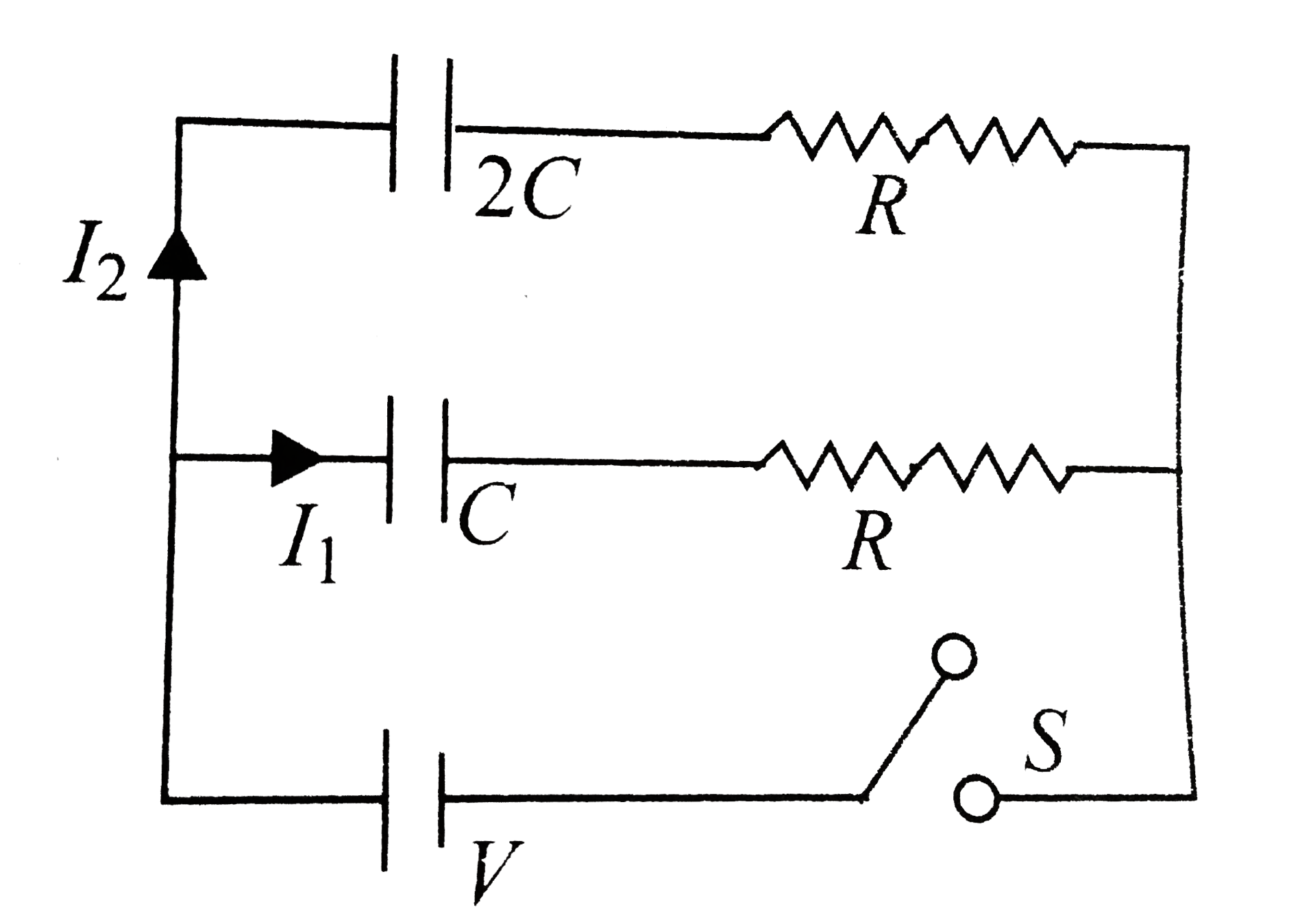
View SolutionIn the circuit shwon in fig. switch S is closed at time t = 0. Let I1andI2 be the currents at any finite time t, then the ratio I1/I2
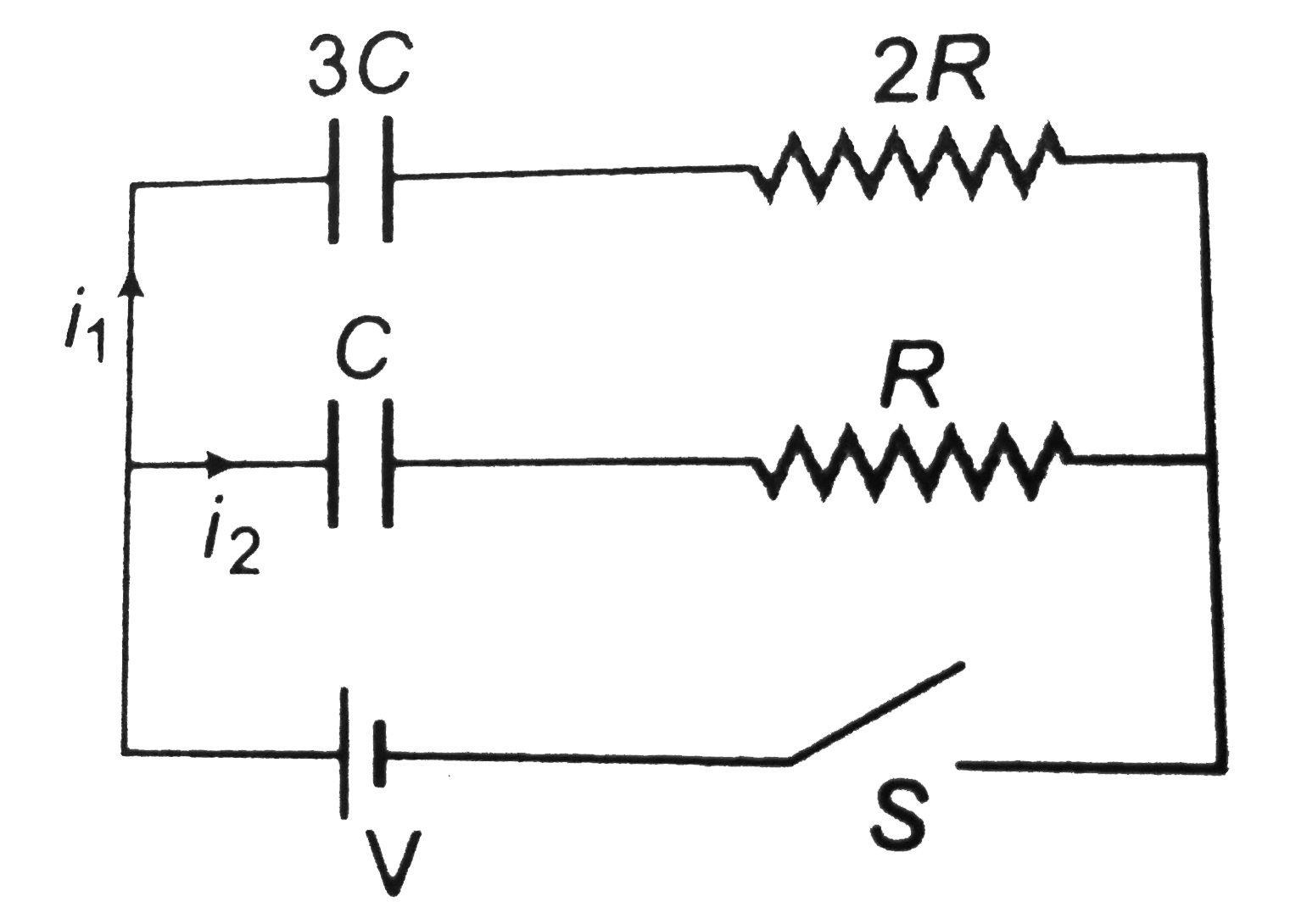
View SolutionIn the circuit shown switch S is closed at t=0. Let i1 and i2 be the current at any finite time t then the ratio i1i2
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given by
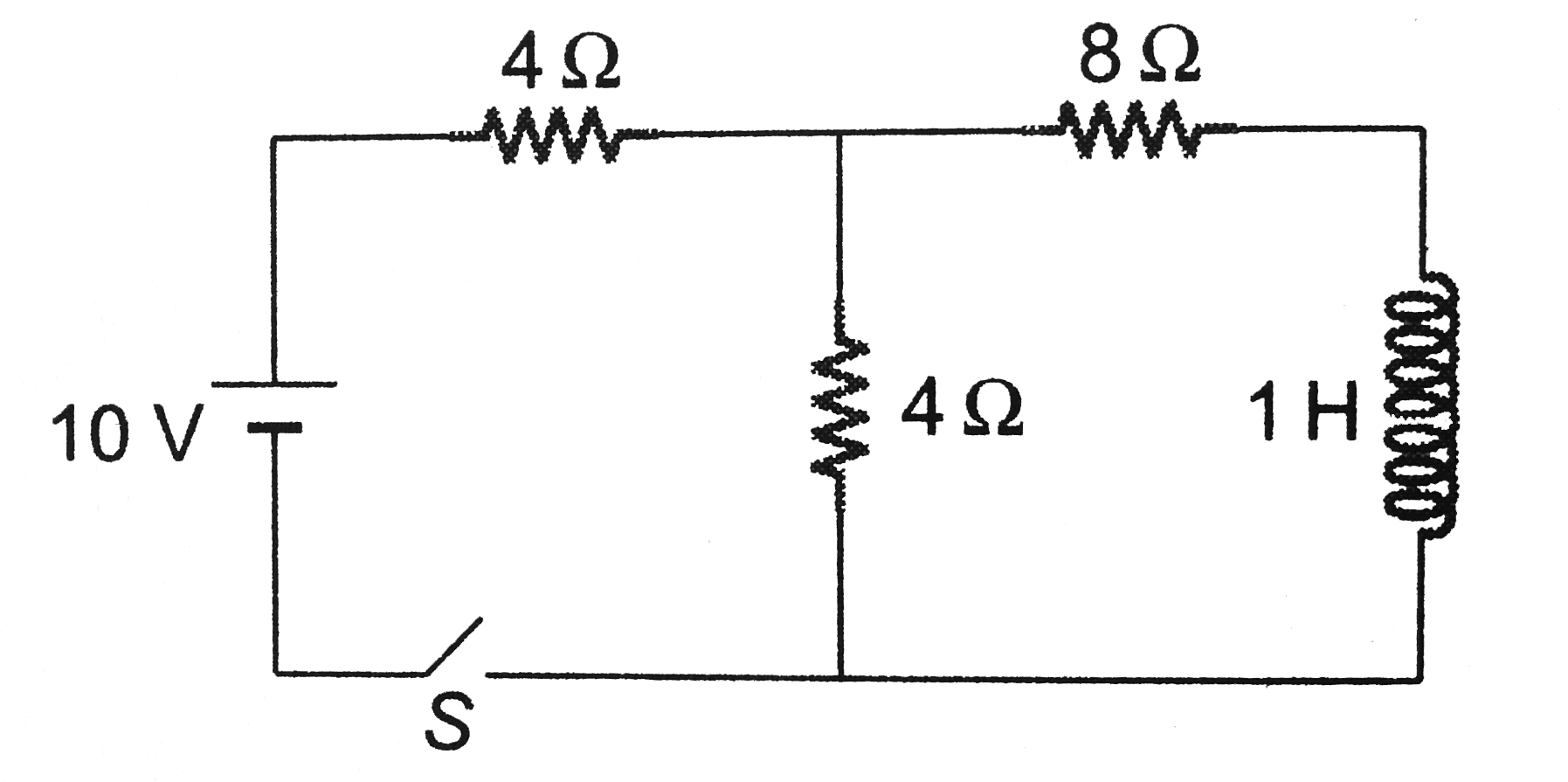
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
View SolutionThe current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second is
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View Solution
