E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that .
Step by step video & image solution for E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that DeltaA B E DeltaC F B . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . Show that ΔABE~ΔCFB .
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F.Show that ΔABE~ΔCFB.
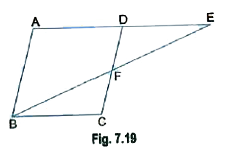
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE~DCFB .
View SolutionE si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
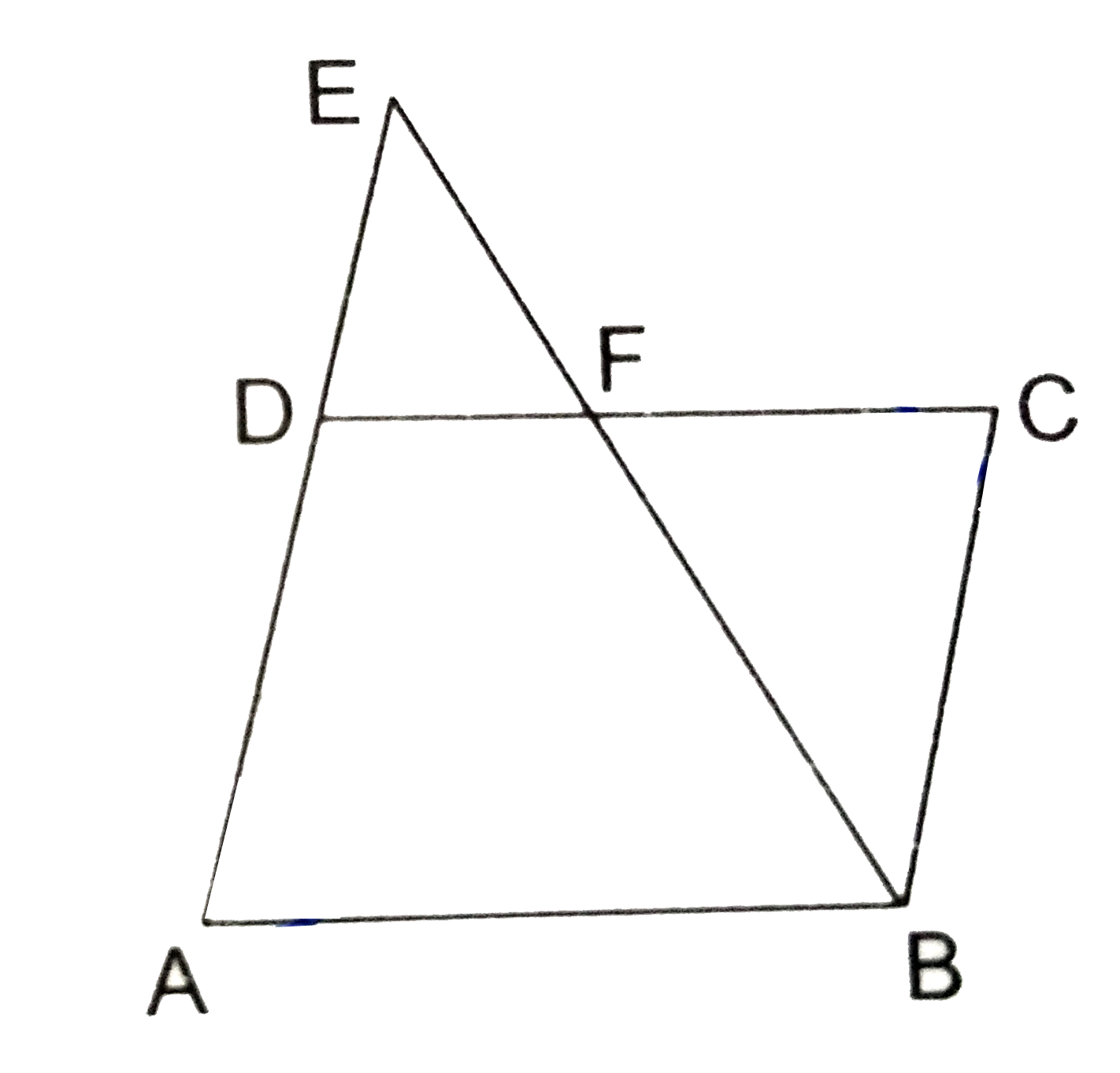
View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
View SolutionABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View Solution
