A conducting disc of mass m and R is given charges +Q and -Q at its topmost and bottom-most point.At t=0 electric field bar(E)=bar(E)_(0)hat l is switched on at t=0 and disc starts rolling without slippage.Friction force acting on the disc at t=0 is (n)/(g)QE_(0) .Find the value of n .(Disc is in vertical plane)
Step by step video & image solution for A conducting disc of mass m and R is given charges +Q and -Q at its topmost and bottom-most point.At t=0 electric field bar(E)=bar(E)_(0)hat l is switched on at t=0 and disc starts rolling without slippage.Friction force acting on the disc at t=0 is (n)/(g)QE_(0) .Find the value of n .(Disc is in vertical plane) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A non conducting solid sphere of mass m and radius R having uniform charge density +ρ and −ρ as shown in figure. It is then placed on a rough non conducting horizontal plane. At t=0 a uniform electric field →E=E0ˆiN/C is switched on and the solid sphere starts rolling with sliding. The magnitude of frictional force at t=0 is 2ρπR3E0K. Find the value of K

View SolutionA nonconducting ring of mass m and radius R, with charge per unit length λ is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field →E=E0ˆi is switched on and the ring starts rolling without on and the ring starts rolling without sliding. Determine the friction froce (magnitude and direction ) acting on the ring.

View Solution
Knowledge Check
A uniform disc of mass m and radius R is thrown on horizontal law in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
Av209gB5v209gCv203gD3v208gA conducting disc of radius R is placed in a uniform and constant magnetic field B parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are e and m)
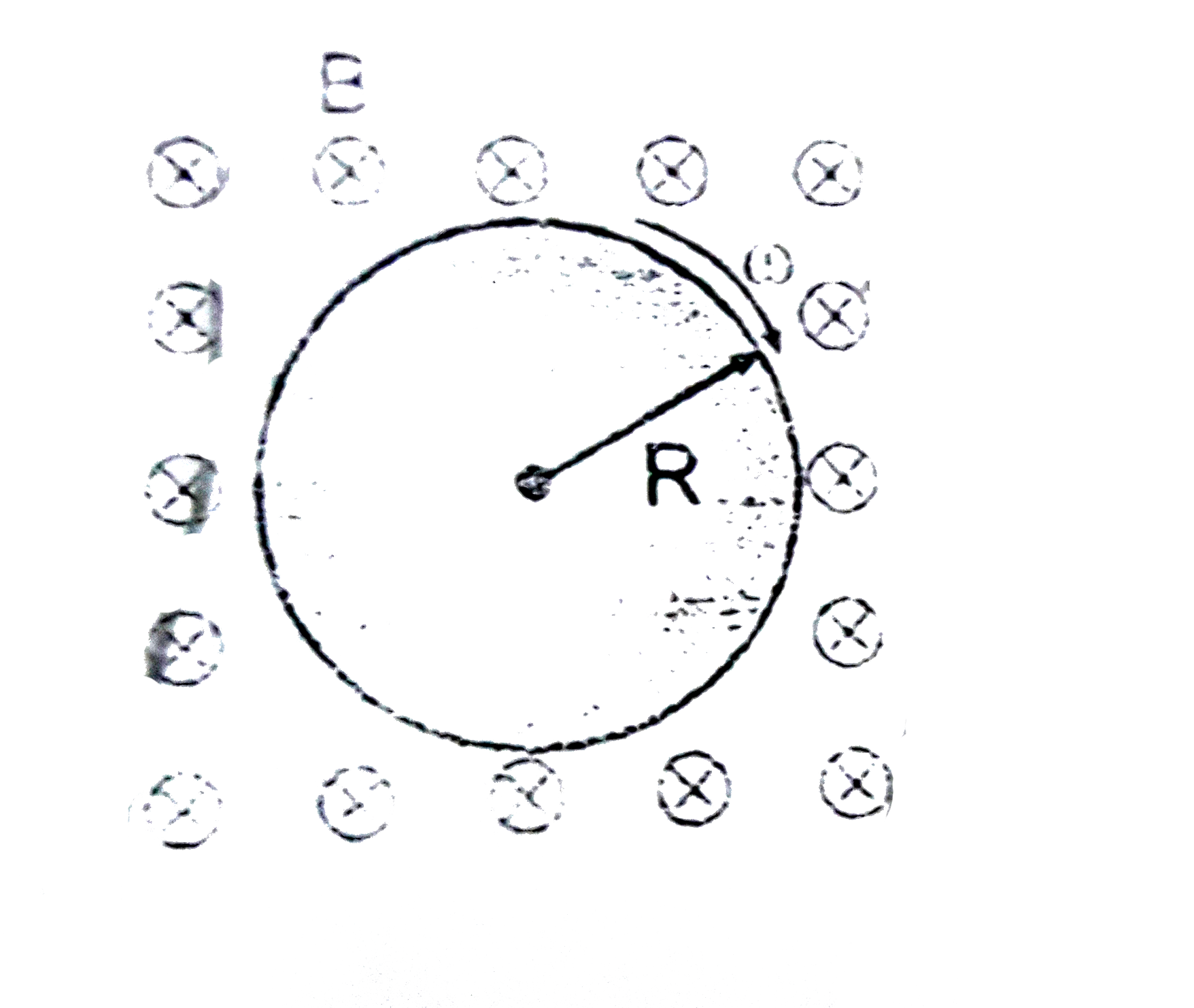 AeB2mBeBmC2πmeBDπmeB
AeB2mBeBmC2πmeBDπmeBA spring of spring constant 'K' is fixed at one end has a small block of mass m and charge q is attached at the other end. The block rests over a smooth horizontal surface. A uniform and constant magnetic field B exists normal to the plane of paper as shown in figure. An electric field →E=E0ˆi(E0 is a positive constant) is switched on at t=0 sec. The block moves on horizontal surface without ever lifting off the surface. Then the normal reaction acting on the block is :
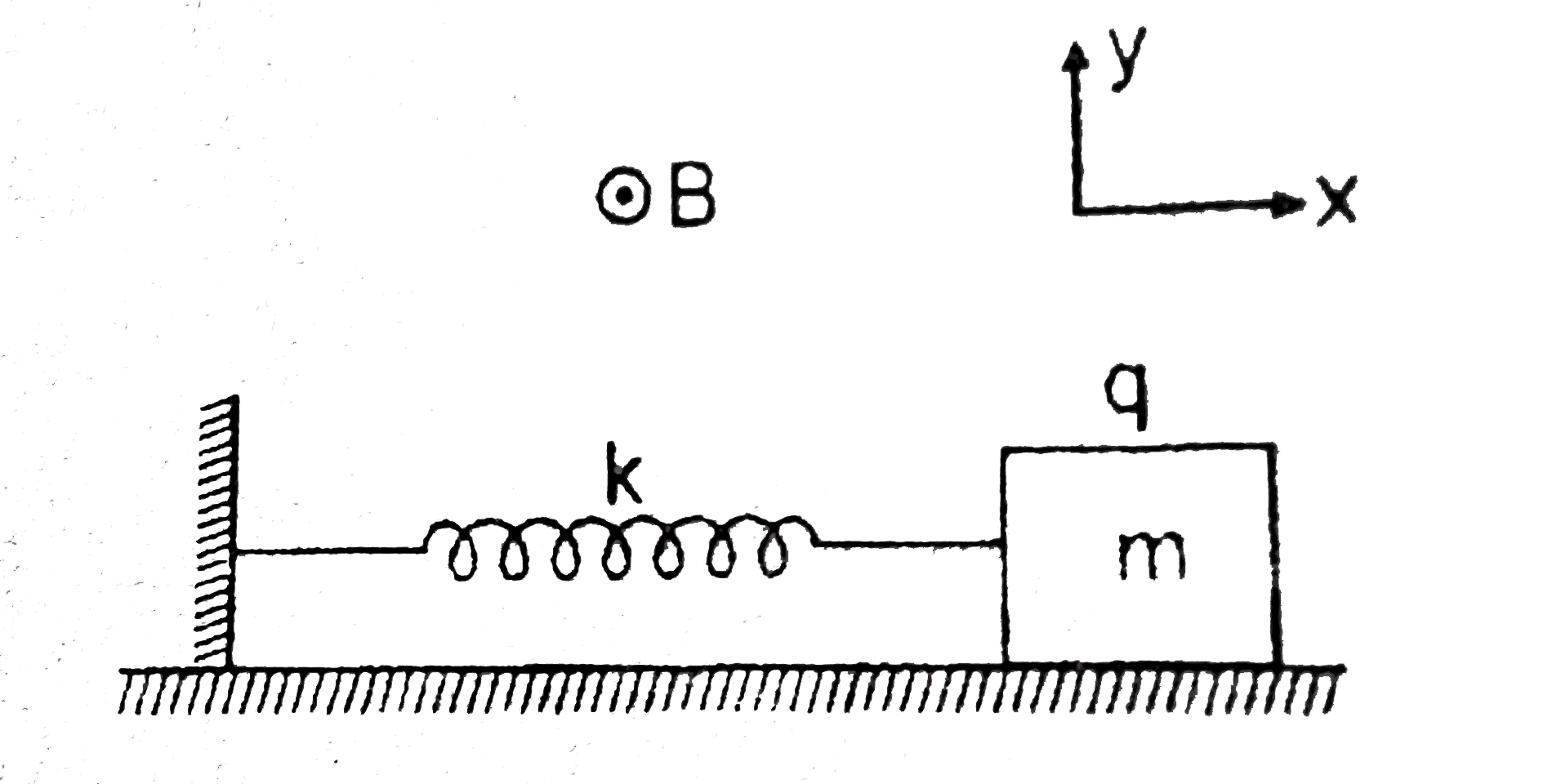 AMaximum at extreme position and minimum at mean positionBMaximum at mean position and minimum at extreme positionCis uniform throughout the motionDIs both maximum and minimum at mean position
AMaximum at extreme position and minimum at mean positionBMaximum at mean position and minimum at extreme positionCis uniform throughout the motionDIs both maximum and minimum at mean position
A nonconducting ring of mass m and radius R is charged as shown. The charged density i.e. charge per unit length is λ. It is then placed on a rough nonconducting horizontal surface plane. At time t = 0, a uniform electric field →E=E0ˆi is switched on and the ring starts rolling without sliding. The friction force (magnitude and direction) acting on the ring, when it starts moving is
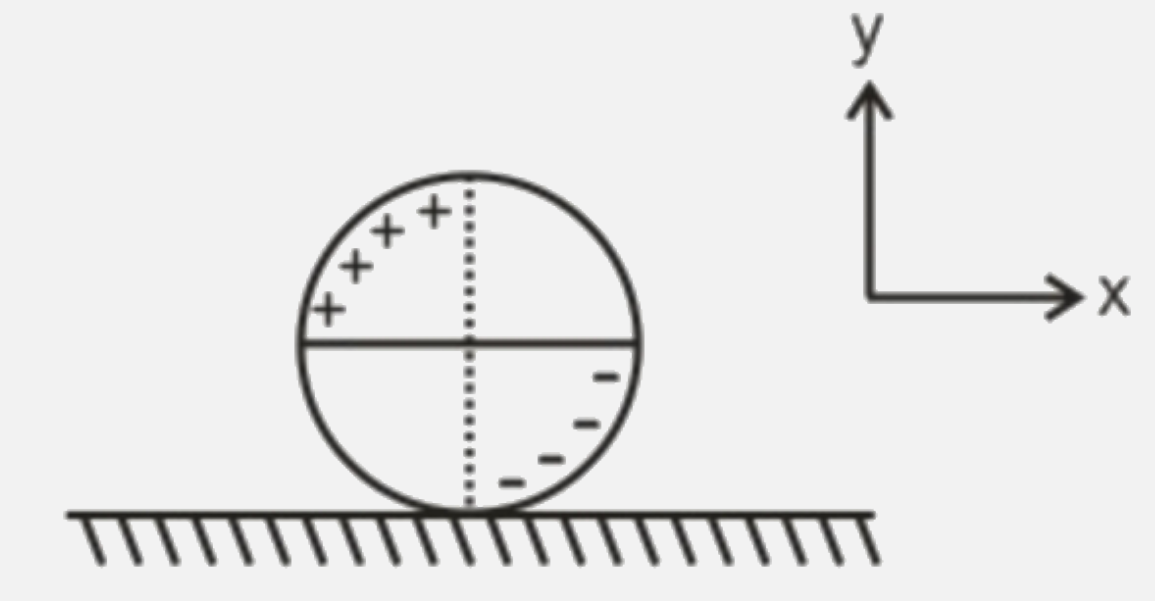
View SolutionA dielectric disc of radius R and uniform positive surface charge density σ is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is qm=4εon0gσ.
(i). Find the value of H if the particle just reaches the disc.
(ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position.
View SolutionIn each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At t=0 (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and ω0 and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.

View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
View SolutionA disc of mass m is connected with an ideal spring of spring constant k inside a lift as shown. The left starts moving with constant acceleration (aˆi−aˆj). At the same moment disc starts rolling without sliding on the wall of lift (from rest). If spring is in natural length initially then friction force acting on disc as a function of y is given by : (y is the displacement of the disc with respect to lift)

View Solution
