A thin non conducting horizontal disc of mass $m$ having total charge $q$ distributed uniformly over its surface, can rotate freely about its own axis. Initially when the disc is stationery a magnetic field $B$ directed perpendicular to the plane is switched on at $t = 0$ . Find the angular velocity $ω$ acquired by disc as a function of time, if $B = k t$ , where $t$ is time.

Video Solution

Text Solution

Verified by Experts

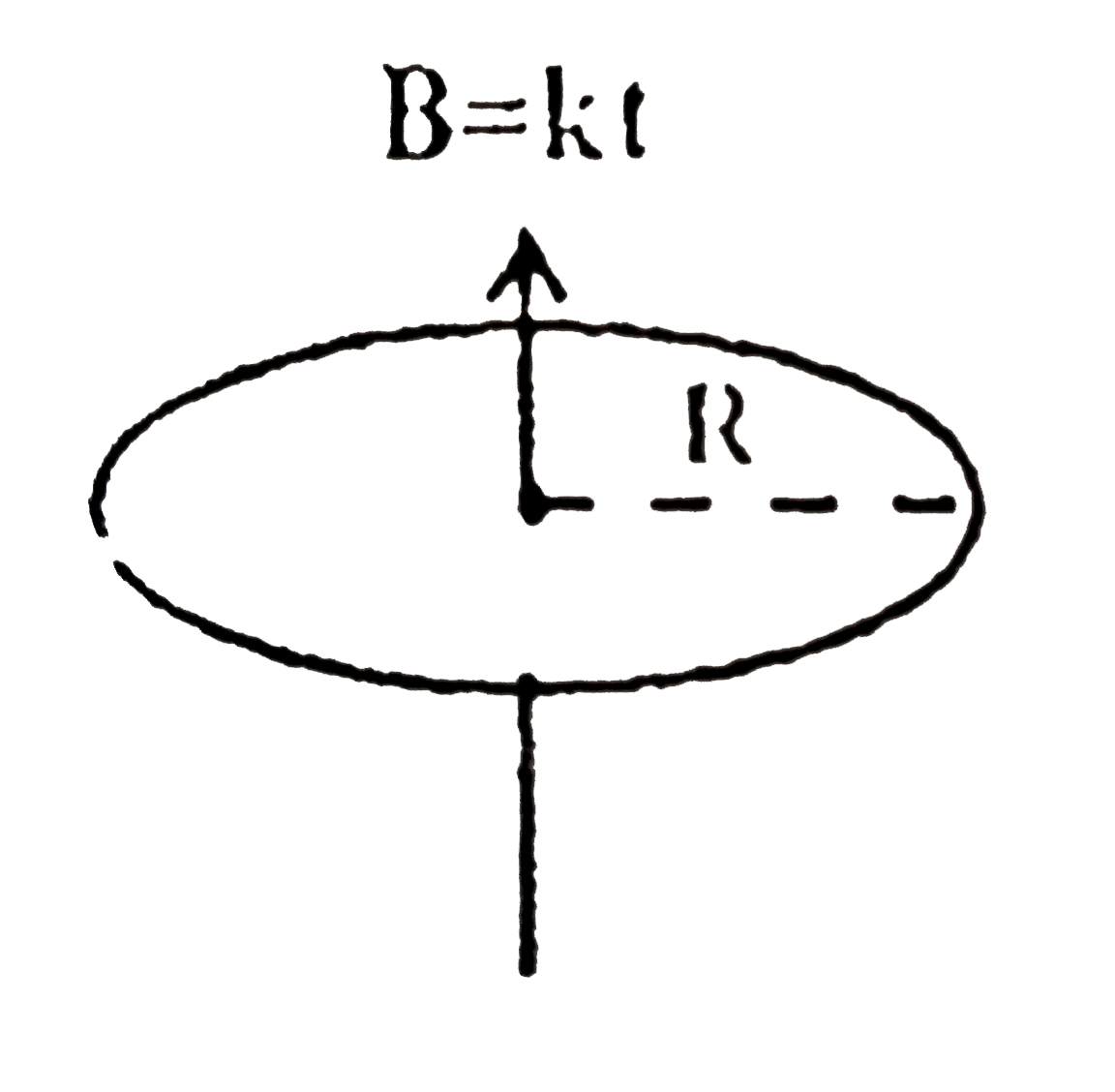
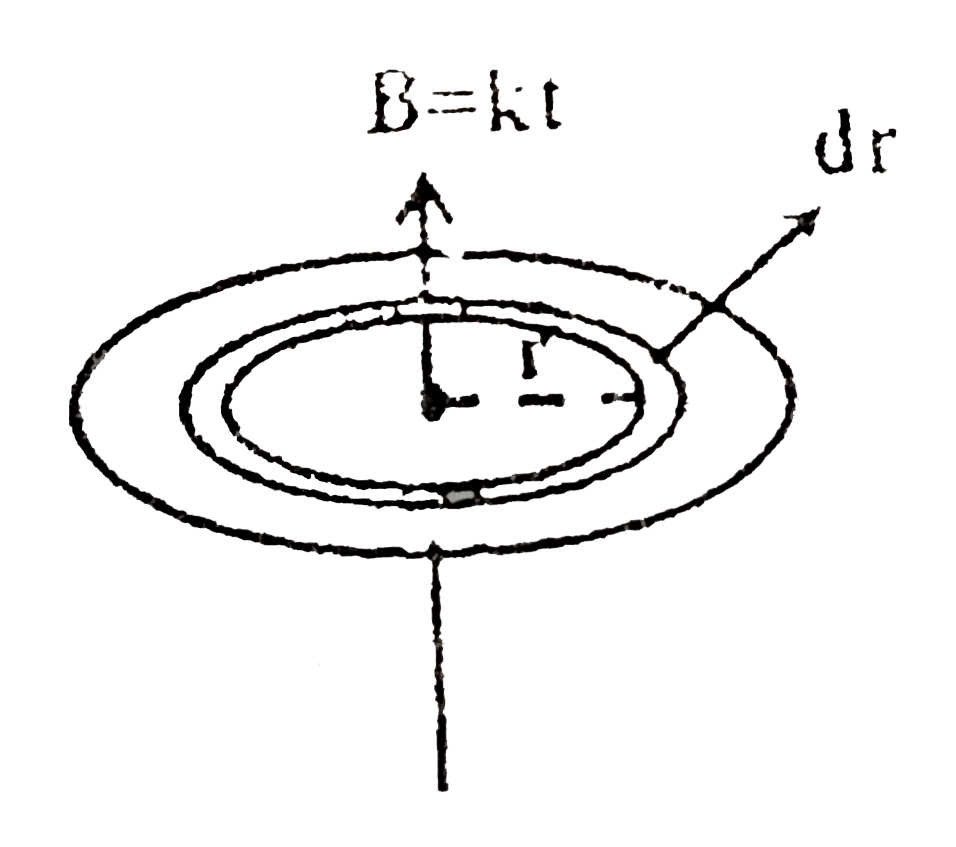
Consider a ring of radius $r$ , width $d r$ and charge on ring
$d q = (2 π r d r) - \frac{Q}{π R^{2}}$
Induced emf in ring
$ε = \oint \vec{E} . d \vec{l} = - \frac{- d}{d t} \int \vec{B} . d \vec{S}$
Let $E$ is electric field in circular loop.
Then $E .2 π = - π r^{2} \frac{d B}{d t} = - π r^{2} k$
$∴ E = - \frac{r . k}{2}$
Force on the ring $= d F = d q E = - (d q) \frac{r k}{2}$
Torque $τ = \int_{0}^{R} r d F = \int_{0}^{R} r (\frac{2 π Q d r}{π T^{2}}) \frac{r k}{2} = \int_{0}^{R} \frac{k Q r^{3}}{R^{2}} d r = \frac{- k Q R^{2}}{4} = I α$
$∴ α = - \frac{k Q R^{2}}{4 (m R^{2} / 2)} = \frac{- k Q}{2 m}$
$∴ ω = - \frac{k Q}{2 m} t$
$∴ | ω | = \frac{k Q}{2 m} t$

Updated on:21/07/2023

A disc of mass $m$ has a charge $Q$ distributed on its surface. It is rotating about an $X X'$ with a angular velocity $ω$ . The force acting on the disc is

Azero
B $ω R B / π$
C $2 Q ω B R$
Dnone of these
A ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
A $\frac{q B}{m}$
B $\frac{2 q B}{m}$
C $\frac{q B}{2 m}$
DNone of these
A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity $ω$ . The magnetic moment of the arrangement is
A $\frac{Q R^{2} ω}{8}$
B $\frac{Q R^{2} ω}{4}$
C $\frac{Q R^{2} ω}{2}$
DZero