A printed page is kept pressed by a transparent cube of edge t. The refractive index of the cube varies us μ(z)=1+zt, where x is the vertical distance from bottom of the cube. If viewed from top, then the printed letters appear to be shifted by an amount
(1−ln2)t
(2ln2−1)t
t2ln2
2t3ln2
The correct Answer is:A
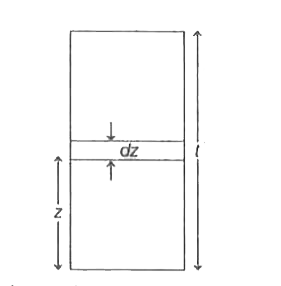
Condider an elemental strip at a height z of thickness dz.
Apparent height =Real height RI=dμ(z)
dh=dz1+zt
dh=(tt+z)dz
h∫z0tt+z.dz
h=[tln(t+z)]20=t[ln(1+t)−ln(t+0)]
h=tln2tt=tln2
Shift, Δx,=t−tln2
⇒Δx=(1−ln2)t
Topper's Solved these Questions
Similar Questions
A printed page is kept pressed by a glass cube (μ=1.6) of edge 6.0cm. By what amount will the printed letters appear to be shifted when viewed from the top ?
View SolutionA printed page is kept pressed by a glass cube (µ=1.5) of edge 9.0 cm. By what amount will the printed letters appear to be shifted when viewed from the top?
View Solution
Knowledge Check
A printed page is pressed by a glass of water. The refractive index of the glass and water is 1.5 and 1.33, respectively. If the thickness of the bottom of glass is 1 cm and depth of water is 5 cm, how much the page will appear to be shifted if viewed from the top?
A1.033 cmB3.581 cmC1.3533 cmD1.90 cmA small air bubble is inside a transparent cube of side length 24 cm and of refractive index 43 If the apparent distance air bubble from a face is 9 cm then its apparent distance from opposite face is
A6cmB8cmC9cmD12cmA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1andn2(>n1), as shown in the figure. A ray of light is incident with angle θi, from medium 1 and emerges in medium 2 with refraction and θf, with a lateral displacement l.
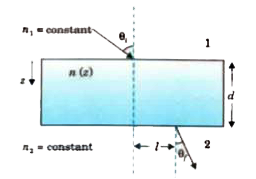
Which of the following statement(s) is (are) true ?Al is independent of n2Bn1sinθ1=n2sinθfCl is independent of n(z)Dn1sinθ1=(n2−n1)sinθf
A printed page is kept pressed by a glass cube (µ=1.5) of edge 9.0 cm. By what amount will the printed letters appear to be shifted when viewed from the top?
View SolutionA printed page is kept pressed to a glass cube (μ=1.5) of edge 6.0 cm. By what amount will the printed letters appear to the shifted when viewed from the top?
View SolutionA printed page is kept pressed to a glass cube (μ=1.5) of edge 6.0 cm. By what amount will the printed letters appear to the shifted when viewed from the top?
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2(>n1), θ0, from medium 1 and emerges in medium 2 with refraction angle θtwith a lateral displacement l.
Which of the following statement(s) is (are) true?
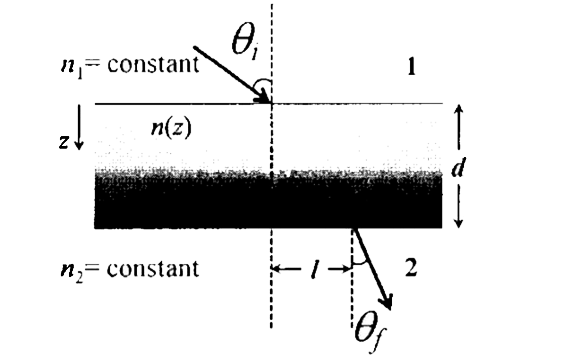
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2(>n1), θi, from medium 1 and emerges in medium 2 with refraction angle θfwith a lateral displacement l.
Which of the following statement(s) is (are) true?

View Solution
