A square loop of length L is placed with its edges parallel to the XY-axies. The loop is carrying the current I. If the magnetic field in the region varies as B=B0(1+xyL2)ˆk, then the magnitude of the force on the loop willl be
lB0L
lB0L2
lB0L√2
√2lB0L
(∗)We take one vertex of square loop at origin,
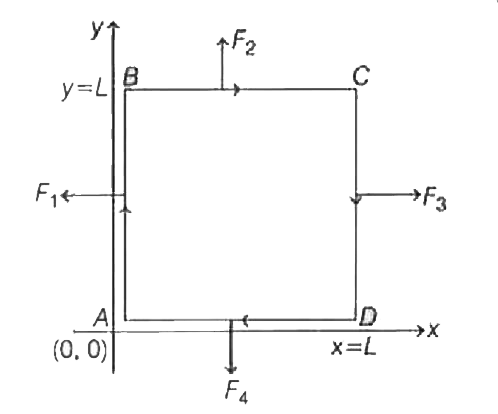
for wire AB, magnetic field AB=B0(1+0)=B0,
∴n=0
For wire CD, magnetic fiels =B0(1+yL),
∴x=L
For wire BC, magnetic field =B0(1+xL),
and for wire AD, magnetic field =B0
∴y=0
Now me calculate forces
F1,F2,F3andF4,
F1=∫L0IB0dy=IB0L
F2=∫I0IB0(1+xL)dx=32IB0L
F3−∫L0IB0(1+yL)dx
=32IB0L
F4=∫L0IB0dx=IB0L
Topper's Solved these Questions
Similar Questions
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πaA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to L
A square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
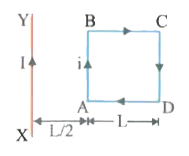
View SolutionA square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be

View SolutionA square loop ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
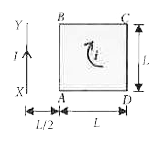
View Solution
A square loop ABCD carrying a current i is placed near and coplanar with a long straight conductor XY carrying a current I.
View SolutionA closed loop lying in the xy plane carries a current. If a uniformn magnetic field B is present in the region, the force acting on the loop will be zero, if B is in
View Solution
