A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
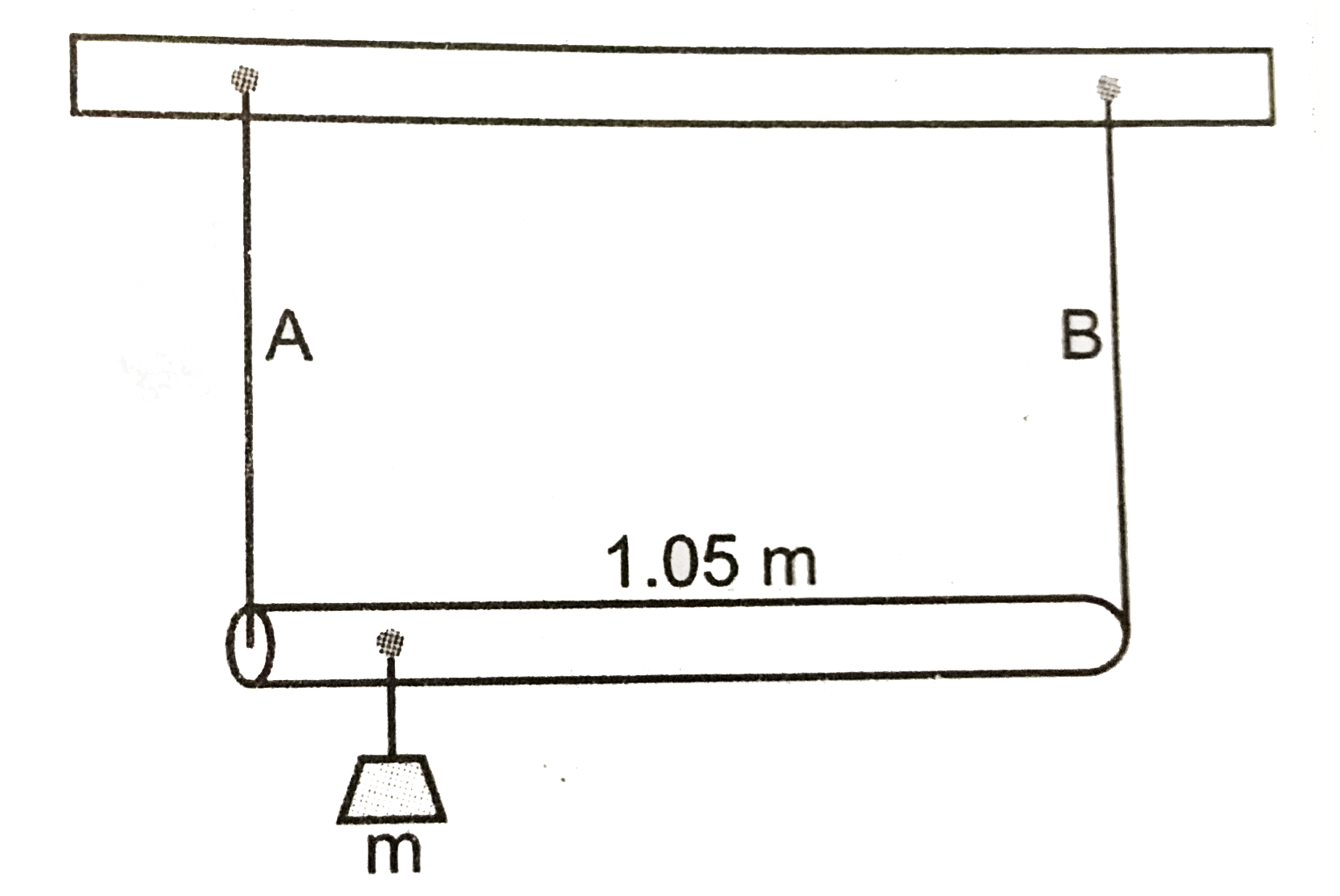
Mass m should by suspended close to wire A to have equal stresses in both the wires
Mass m should be suspended close to B to have equal stresses in both the wires
Mass m should be suspended at the middle of the wires to have equal stresses in both the wires
Mass m should be suspended close to wire A to have strain in both wires
The correct Answer is:B, D
Let the mass is placed at x from the end B.

Let TA and TB be the tensions in wire A and wire B respectively.
For the rotational equilibrium of the system,
Στ=0 (Total torque = 0)
⇒ TBx−TA(l−x)=0
⇒ TBTA=l−xx ....(i)
Stress in wire A=SA=TAaA
Stress in wire B=SB=TBaB
where aA and aB are cross-sectional areas of wire A and B respectively.
By equation aB=2aA
Now, for equal stress SA=SB
⇒ TAaA=TBaB⇒TBTA=aBaA=2
⇒ l−xx=2⇒lx−1=2
⇒ x=l3⇒l−x=l−l/3=2l3
Hence, mass m should be placed closer to B.
For equal strain, (Strain)A=(Strain)B
⇒(YA)SA=YBSB (where YA and YB are Young modulii)
⇒YsteelTA/aA=YAlTB/aB
⇒ YsteelYAl=TATB×aBaA=(xl−x)(2aAaA)
⇒ 200×10970×109=2xl−x⇒207=2xl−x
⇒ 107=xl−x⇒10l−10x=7x
⇒ 17x=10l⇒x=10l17
l−x=l−10l17=7l17
Hence, mass m should be placed closer to wire A.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LONG SHORT ANSWER TYPE QUESTION
16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLARCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions
3 Videos
- MOTION IN A PLANEBOOK - NCERT EXEMPLARCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions
37 Videos
Similar Questions
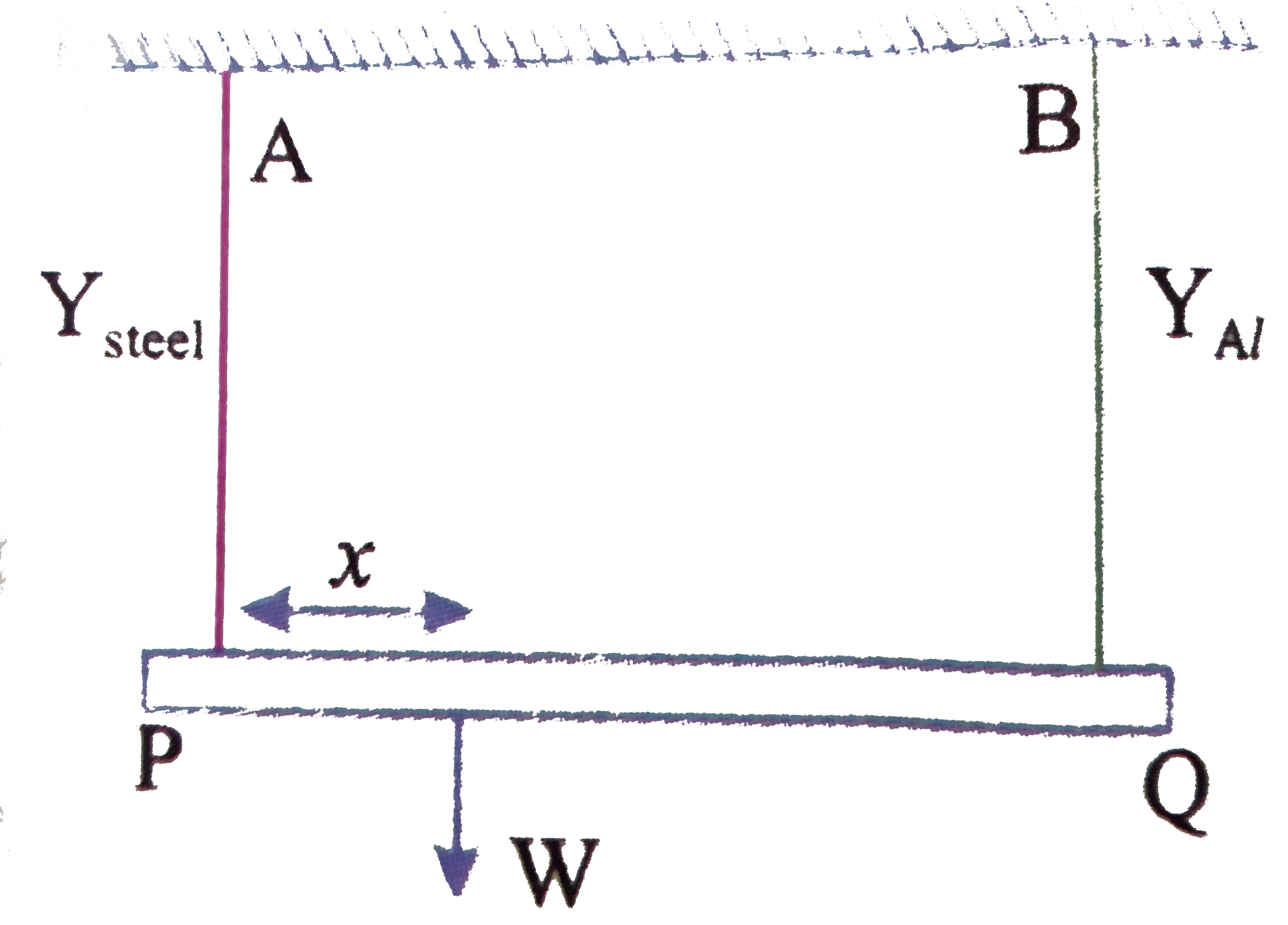
A rod PQ of length 1.05m having negligible mass is supported at its ends by two wires one of stell (wire A), and the other of aluminium (wire B) of equal lengths as shown in fig. The cross-sectional areas of wires A and B are 1.0mm2 and 2.0mm2 respectively. At what point along the rod a load W be suspended in order to produce
(a) equal stress, (b) equal strains in both steel an aluminium.
(Ysteel=200GPa,Yaluminium=70GPa)
View SolutionA point mass m is suspended usin two wires of different material as shown in the figure. If corss-section of wire-1 and sore-2 are 3mm2and√3mm2 respectively, which of the following is correct?

View Solution
Knowledge Check
A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
 AMass m should be suspended close to wire A to have equal stresses in both the wires.BMass m should be suspended close to B to have equal stresses in both the wires.CMass m should be suspended at the middle of the wires to have equal stresses in both the wires.DMass m should be suspended close to wire A to have equal strain on both wires.
AMass m should be suspended close to wire A to have equal stresses in both the wires.BMass m should be suspended close to B to have equal stresses in both the wires.CMass m should be suspended at the middle of the wires to have equal stresses in both the wires.DMass m should be suspended close to wire A to have equal strain on both wires.A light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that
A20m/sB25m/sC22m/sD18m/sTwo wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
Alight rod of length 2 m is suspended horizontlly from the ceiling bty means of two vertical wirs of equal length tied to its ends One wire is mode of steel and is of cross - section 0.1 sq cm and the other is of brass of cross -section 0.2 sq cm Find the postion along the rod at which a wight may be hung to produce (i) equal stress in both wirs (ii) equal strain in both wires (Y for brass =10×1010Nm−2andYfor steel=20×1010Nm−2)
View SolutionA light rod of length 4.0 m is suspended from the ceiling horizontally by means of two vertical wire of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. Find out the position along the rod at which a weight may be hung to produce equal stresses in both wires.
View SolutionTwo wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View SolutionA light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that of B. A weight W is hung on the rod as shown. The value of x, so that the stress In A is same as that in B,is

View SolutionA light rod of length 200 cm is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross- section 0.1 cm2 and the other of brass of cross-section 0.2 cm2 . Along the rod at which distance a weight may be hung to produce equal stresses in both the wires ?
View Solution
