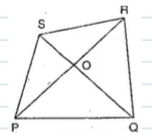
In Figure, PQRS
is a quadrilateral in which diagonals PR
and QS
intersect in O
. Show that
PQ+QR+RS+SP>PR+QS
PQ+QR+RS+SP<2 (PR+QS)
Step by step video & image solution for In Figure, P Q R S is a quadrilateral in which diagonals P R and Q S intersect in O . Show that P Q+Q R+R S+S P > P R+Q S PQ+QR+RS+SP<2 (PR+QS) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
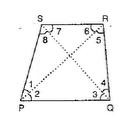
In Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View Solution
Knowledge Check
IF p q r s are in harmonic progression and p>s then
A1ps<1qrBq+r=p+sC1q+19=1r+1sDnone
If PQRS is a square, then write the measure of ∠SRP
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
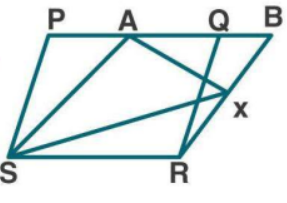
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
View SolutionGIVEN : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. TO PROVE : (i) ∠R>∠P (ii) ∠S>∠Q CONSTRUCTION : Join PR and QS. Figure
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

View Solution
