AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
Given: AC=BC
∠PCA=∠PCB=90∘
To prove: PA=PB
Proof: In △PCA and △PCB
AC=BC [Given]
∠PCA=∠PCB=90∘ [Given]
PC=PC [common]
△APC≅△ABC [SAS]
⇒PA=PB
Hence proved.
Topper's Solved these Questions
Similar Questions
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionAB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionA line segment is symmetrical about its perpendicular bisector.True or false?
View SolutionTo construct the perpendicular bisector of a given line segment.
View SolutionDraw perpendicular bisector to line segment AB if l(AB)=7cm.
View SolutionIn the given figure, AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
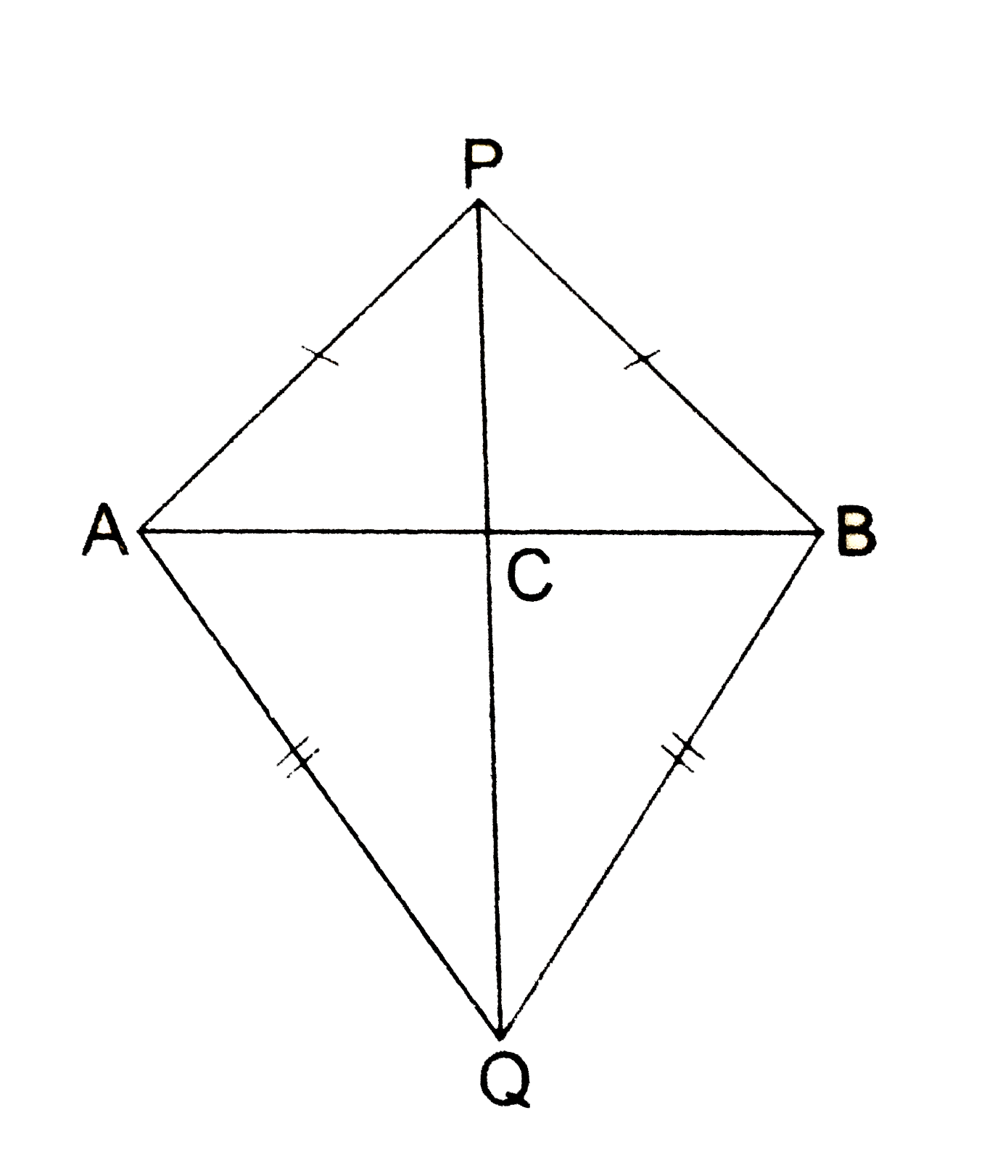 View Solution
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
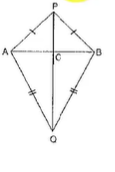 View Solution
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB . Show that l bisects CD.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View Solution

