In Fig. 10.64, BC is a tangent to the circle with centre O.OE bisects AP. Prove that ΔABC~ΔAEO
∠AEOand∠PEO
OE=OE(same)
CP=EA(given)
OA=OD(radius)
∠AEo≅∠PEO
∠AEO=∠PEO=900
∠AEOand∠ABC
∠A=∠A(common)
∠AED=∠ABC=900
∠AEO≅∠ABC(AAsimilarity)
Similar Questions
In a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn a right triangle ABC, a circle with a side. AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent to the circle at P bisects the side BC.
View SolutionIn the figure, an isosceles triangle ABC with AB=AC circumscribes a circle. Prove that the point of contact P bisects the base BC.
View SolutionIn a right-triangle ABC in which ∠B=90∘, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
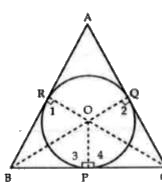
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
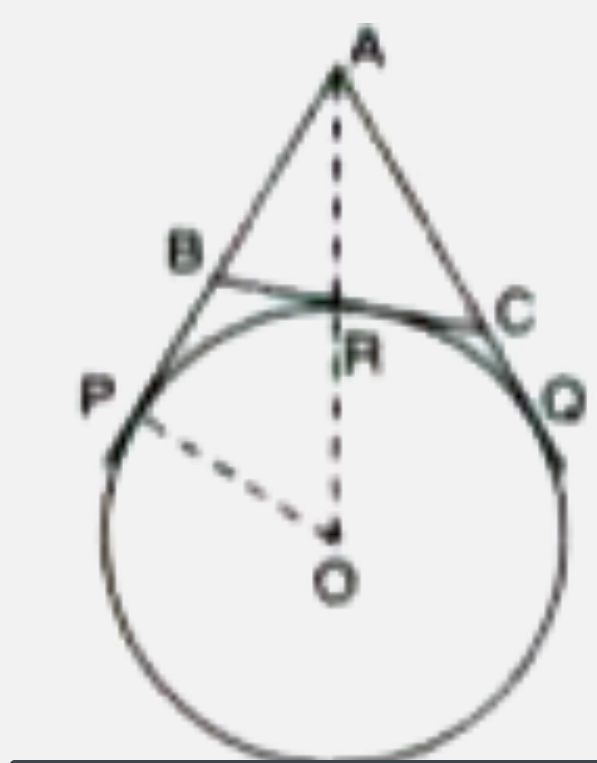
View SolutionIn a right triangle ABC, a circle with AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent at P, bisects the side BC.
View Solution
