The excess temperature of a hot body above its surroundings is halved in t = 10 minutes. In what time will it be 110 of its initial value. Assume Newton's law of cooling.
Using Newton's law of cooling we have
(T−Ts)=(T0−Ts)e−kt
at t=10min(T−Ts)=T0−Ts2
⇒e−k(10)=12
or k=In(2)10 Then at t=t0
T−Ts=T0−Ts10
⇒e−kt0=110
t0In(10)In(2)×10
=33.23 min
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.4
5 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Discussion Question
26 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.2
8 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
The excess temperature of a body falls from 12∘C to 6∘C in 5 minutes, then the time to fall the excess temperature from 6∘C to 3∘C is (assume the newton's cooling is valid)
View SolutionA body cools from 60∘C to 40∘C in 7 minutes. Temperature of surrounding is 10∘C. After next 7 minutes what will be its temperature ? During whole process Newton's law of cooling is obeyed.
View Solution
Knowledge Check
The excess temperature of a body falls from 12∘C to 6∘C in 5 minutes, then the time to fall the excess temperature from 6∘C to 3∘C is (assume the newton's cooling is valid)
A10 minutesB7.5 minutesC5 minutesD2.5 minutesA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
A(θi−θ0)e−ktB(θi−θ0)In(kt)Cθ0+(θi−θ0)e−ktDθie−kt−θ0The correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
A B
B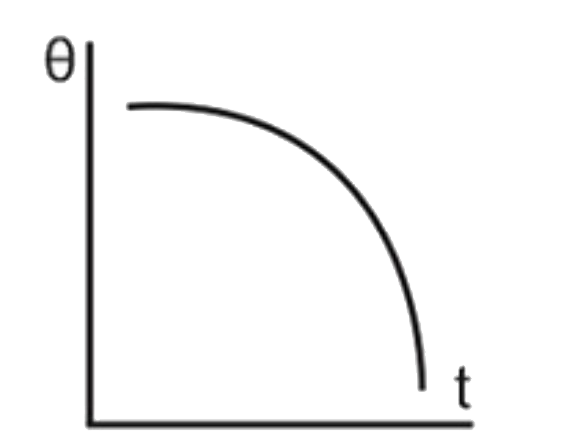 C
C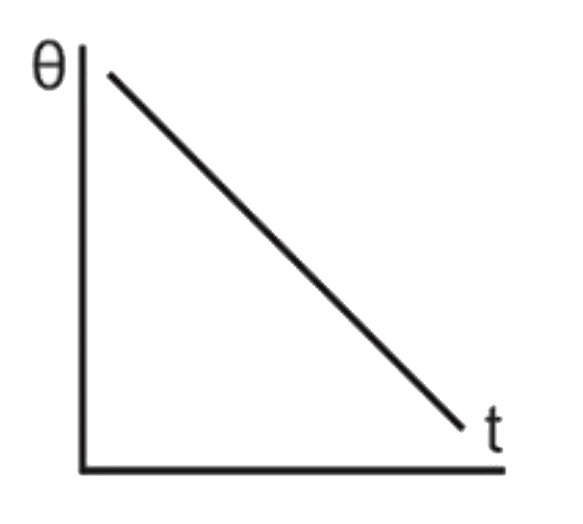 D
D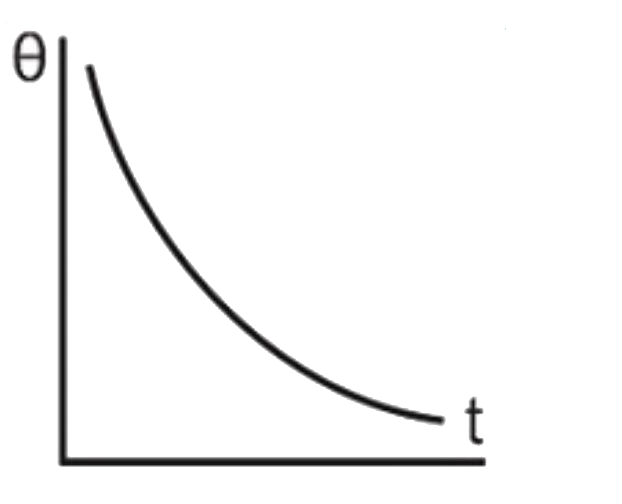
A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionThe correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
View SolutionA body cools from 70∘C to 50∘C in 6 minutes when the temperature of the surrounding is 30∘C. What will be the temperature of the body after further 12 minutes if coolilng proseeds ac cording to Newton's law of cooling ?
View SolutionNewton’s law of cooling says that the rate of cooling of a body is proportional to the temperature difference between the body and its surrounding when the difference in temperature is small.
(a) Will it be reasonable to assume that the rate of heating of a body is proportional to temperature difference between the surrounding and the body (for small difference in temperature) when the body is placed in a surrounding having higher temperature than the body?
(b) Assuming that our assumption made in (a) is correct estimate the time required for a cup of cold coffee to gain temperature from 10∘C to 15∘C when it is kept in a room having temperature 25∘C. It was observed that the temperature of the cup increases from 5∘C to 10∘C in 4 min
View SolutionA body cools from 60%∘C to 50∘C in 10 min. Find its temperature at the end of next 10 min if the room temperature is 25∘C. Assume Newton's law of cooling holds.
View Solution
