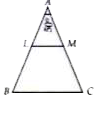
The tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
Video Solution
Text Solution
Let EAF be tangent to the circumcircle of ΔABC
To prove EAF/BC
∠EAB=∠ABC
Here, AB=AC
⇒∠ABC=∠ACB….(i)
[angle between tangent and is chord equal to angle made by chord in the alternate segmaent]
:.Also, ∠EAB=∠BCA....(ii)
From Eqs. (i) and (ii), we get
∠EAB=∠ABC
⇒EAF∣∣BC
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘DE is a tangent to the circumcircle of ΔABC at the vertex A such that DE∣∣BC. If AB=17cm, then the length of AC is equal to
A16.0cmB16.8cmC17.3cmD17cmO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
A3.015 cm.B3.205 cm.C3.025 cm.D3.125 cm.
In an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
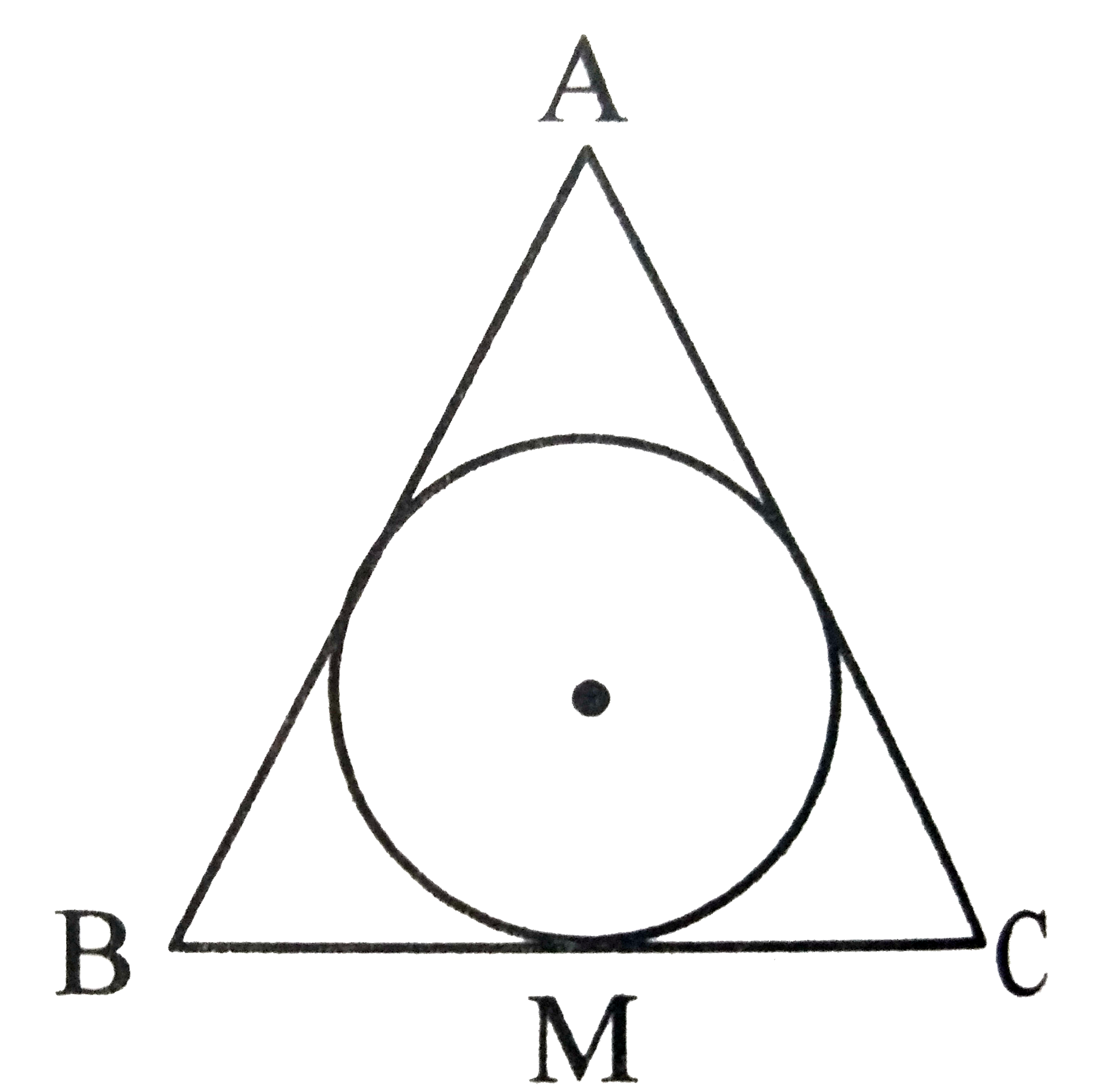
View SolutionIn the adjoining figure, the circle is the incircle of isosceles ΔABC, where seg AB=seg AC. Prove that M bisects BC.
View SolutionFind the area of an isosceles ΔABC in which BC = 8 cm and AB = AC = 5 cm. If CE⊥AB, find CE.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
AD bisects BC
View Solution