If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
Parallelogram
square
Rhombus
Trapezium
The correct Answer is:C
To solve the problem, we need to prove that if in rectangle ABCD, diagonal AC bisects both angle A and angle C, then ABCD is a square.
1. Understanding the Properties of a Rectangle:
- A rectangle has opposite sides that are equal and all angles are 90 degrees.
2. Given Information:
- Diagonal AC bisects angle A and angle C.
- This means that angle A is divided into two equal angles, and angle C is also divided into two equal angles.
3. Setting Up the Angles:
- Let angle A = 2α (since it is bisected, each part will be α).
- Similarly, let angle C = 2β (since it is bisected, each part will be β).
4. Using the Properties of a Rectangle:
- In a rectangle, angle A and angle C are both 90 degrees.
- Therefore, we can set up the equations:
- 2α = 90 degrees → α = 45 degrees
- 2β = 90 degrees → β = 45 degrees
5. Analyzing the Triangle Formed by the Diagonal:
- Consider triangle ABC formed by points A, B, and C.
- Since angle A = 45 degrees and angle B = 90 degrees, angle C must also be 45 degrees (because the sum of angles in a triangle is 180 degrees).
6. Using the Isosceles Triangle Property:
- In triangle ABC, since angle A = angle C = 45 degrees, it follows that sides AB and BC must be equal (because the angles opposite to equal sides are equal).
7. Conclusion About the Sides:
- Since AB = BC and also AD = DC (as opposite sides of a rectangle are equal), we can conclude that all sides of rectangle ABCD are equal (AB = BC = CD = DA).
8. Final Conclusion:
- Since all sides are equal and all angles are 90 degrees, rectangle ABCD is a square.
Final Answer:
ABCD is a square.
---
- A rectangle has opposite sides that are equal and all angles are 90 degrees.
- Diagonal AC bisects angle A and angle C.
- This means that angle A is divided into two equal angles, and angle C is also divided into two equal angles.
- Let angle A = 2α (since it is bisected, each part will be α).
- Similarly, let angle C = 2β (since it is bisected, each part will be β).
- In a rectangle, angle A and angle C are both 90 degrees.
- Therefore, we can set up the equations:
- 2α = 90 degrees → α = 45 degrees
- 2β = 90 degrees → β = 45 degrees
- Consider triangle ABC formed by points A, B, and C.
- Since angle A = 45 degrees and angle B = 90 degrees, angle C must also be 45 degrees (because the sum of angles in a triangle is 180 degrees).
- In triangle ABC, since angle A = angle C = 45 degrees, it follows that sides AB and BC must be equal (because the angles opposite to equal sides are equal).
- Since AB = BC and also AD = DC (as opposite sides of a rectangle are equal), we can conclude that all sides of rectangle ABCD are equal (AB = BC = CD = DA).
- Since all sides are equal and all angles are 90 degrees, rectangle ABCD is a square.
ABCD is a square.
Topper's Solved these Questions
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - PART-A( True (T) and False (F))
6 Videos
- QUARILATERAL BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - B
12 Videos
- PROBABILITY MIND MAPBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST
6 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PRACTICE TEST
5 Videos
Similar Questions
Knowledge Check
Three statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?AI onlyBII and IIICI and IIIDI and IIThe diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
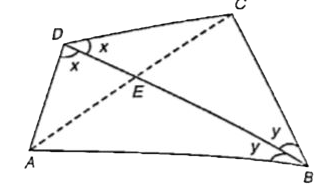 AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
AABCD=ADBCBADAB=BCCDCABBC=ADCDDAB=AD×BC
In a rectangle ABCD, diagonals AC and BD intersect at O. If ∠OAB=35∘, find :
(a)∠ABC(b)∠ABO(c)∠CO(d)∠BOC)
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠B as well as ∠D.
View SolutionIn a rectangle ABCD, the diagonals intersect at O.If ∠AOB=62∘, then ∠ODC=

View SolutionABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
View SolutionIn a cyclic quadrilateral ABCD, diagonal AC bisects ∠C. Prove that the tangent to thecircle at A is parallel to the diagonal BD.
View SolutionIn parallelogram ABCD, diagonals AC and BD are equal. Find the measure of ∠ ABC and prove that the quadrilateral ABCD is a rectangle.
View Solution