An electron files into a homogeneous magnetic field of 10−3 perpendicular to the force lines. The velocity of the electron is v=4×107ms−1 what is the tangential acceleration of electron in the magnetic field ?
7×1015ms−2
7×1013ms−2
7×1014ms−2
zero
The correct Answer is:D
Step by step video, text & image solution for An electron files into a homogeneous magnetic field of 10 ^(-3) perpendicular to the force lines. The velocity of the electron is v = 4 xx 10 ^(7)ms ^(-1) what is the tangential acceleration of electron in the magnetic field ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
An electron is moving with a velocity of 5×107 m/s in a magnetic field of 6×10−4 T perpendicular to it. What is the frequency? Also find the energy of electron in MeV.
View SolutionAn electron enters electric field of 104V/m perpendicular to the field with a velocity of 107m/s. Find the vertical displacement of electron after 2 milliseconds. Mass of electron =9⋅1×10−31kg, charge on electron =1⋅6×10−19C.
View Solution
Knowledge Check
- Question 1 - Select One
The acceleration of any electron due to the magnetic fields is
A3.14×1014m/s2B4.28×1014m/s2C5.56×1012m/s2D6.28×1014m/s2 - Question 2 - Select One
An electron entres a magnetic field whose direction is perpendicualr to the velocity of the electron. Then
AThe speed of the electron will increaseBThe speed of the electron will decreaseCThe speed of the electron will remain the same.DThe velocity fo the electron will remain the same. - Question 3 - Select One
An electron is projected in the magnetic field along the lines of force
AThere will be no effect on the motion of the electron.Belectron speed will increase but the direction will not change.Cthe electron speed will decrease but direction will not changeDnone of these
An electron accelerated by a potential difference V=3 volt first enters into a uniform electric field of a parallel plate capacitor whose plates extend over a length l=6cm in the direction of initial velocity. The electric field is normal to the direction of initial velocity and its strength varies with time as E=αt, where α=3600Vm−1s−1. Then the electron enters into a uniform magnetic field of induction B=π×10−9T. Direction of magnetic field is same as that of the electric field. Calculate pitch of helical path traced by the electron in the magnetic field. (Mass of electron, m=9×10−31kg)
View SolutionIn a uniform magnetic field of 5T, an electron is moving with constant velocity of 15m/s. The force on the electron is
View SolutionAn electron enters a region that contains a magnetic field directed into the page as shown. The velocity vector of the electron makes an angle of 30∘ with the +y axis. What is the direction of the magnetic force on the electron when it enters the field ?
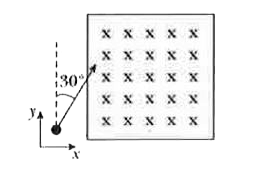 View Solution
View SolutionIf an electron is going in the direction of magnetic field →B with the velocity of →v then the force on electron is
View SolutionAn electron travelloing with a velocity ¯¯¯V=107ˆim/s enter a magnetic field of induction ¯¯¯B=¯¯¯¯2j. The force on electron is
View Solution
