The linear charge density on upper half of semi-circular section of ring is λ and that at lower half is −λ. The direction of electric field at centre O of ring is :

along OA
along OB
along OC
along OD
The correct Answer is:C
Step by step video & image solution for The linear charge density on upper half of semi-circular section of ring is lambda and that at lower half is -lambda. The direction of electric field at centre O of ring is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A semi-infinite insulating rod has linear charge density λ. The electric field atthe pointPshown in figure-1.418 is:

View SolutionA semi-circular wire is charged with linear charge density dependent on the angle θ from +y -axis as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the center of the arc is ¯¯¯E=mKλ04R(−ˆj). Find m.(R is the radius of semi-circle and K=14πɛ0)
'(##CEN_KSR_PHY_JEE_C18_E01_033_Q18##)'
View Solution
Knowledge Check
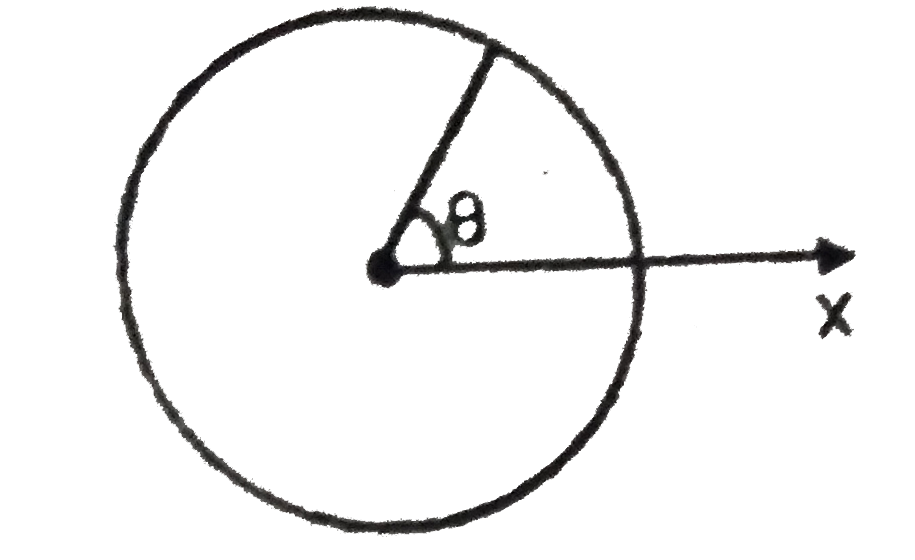
A small element l cut from a circular ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
AzeroBλl4πε0a2C∞Dλ4πεlThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
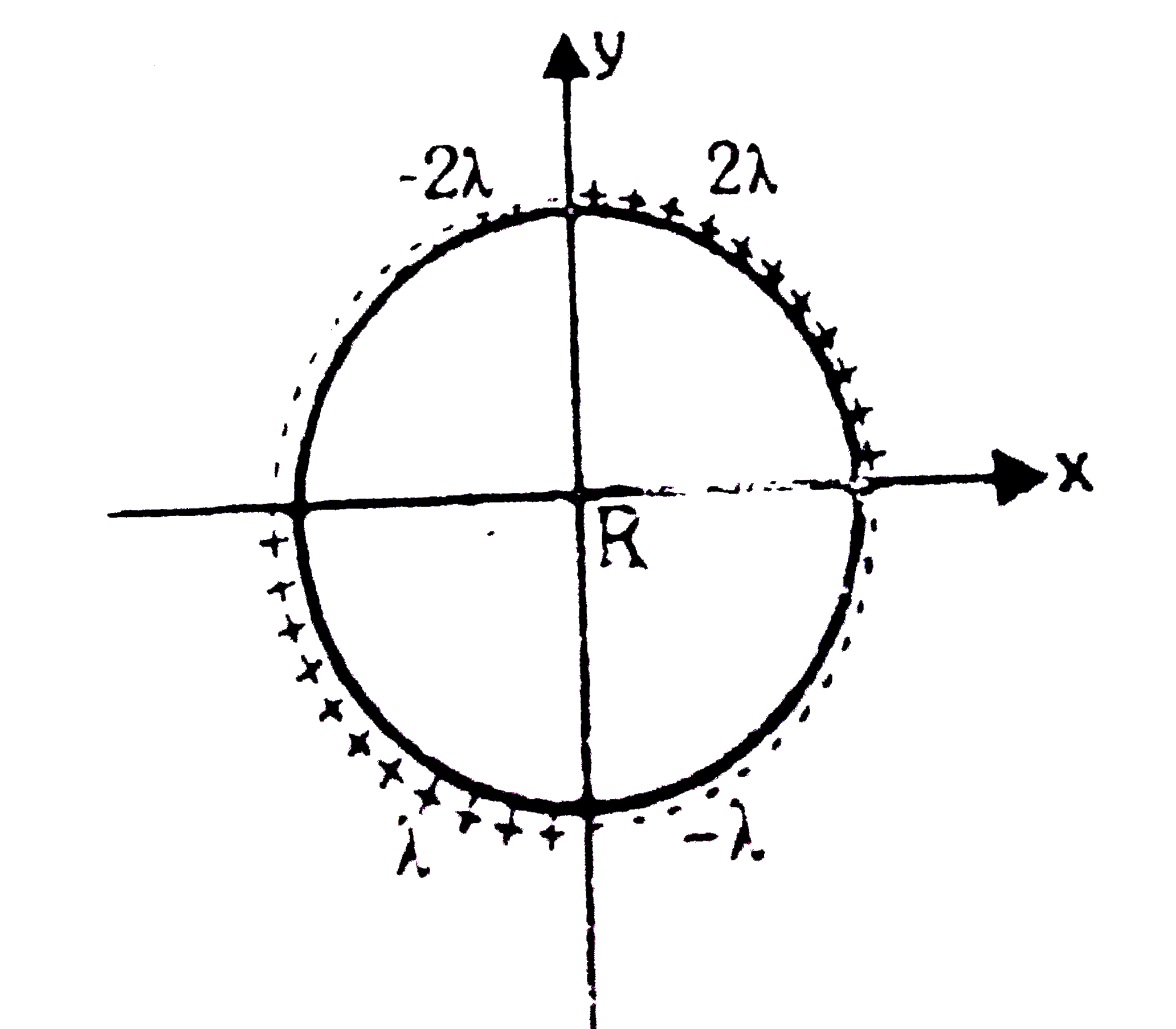 A−λ2πε0RˆiBλ2πε0RˆjC√2λ4πε0RˆiDNone
A−λ2πε0RˆiBλ2πε0RˆjC√2λ4πε0RˆiDNoneIf linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionThe linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
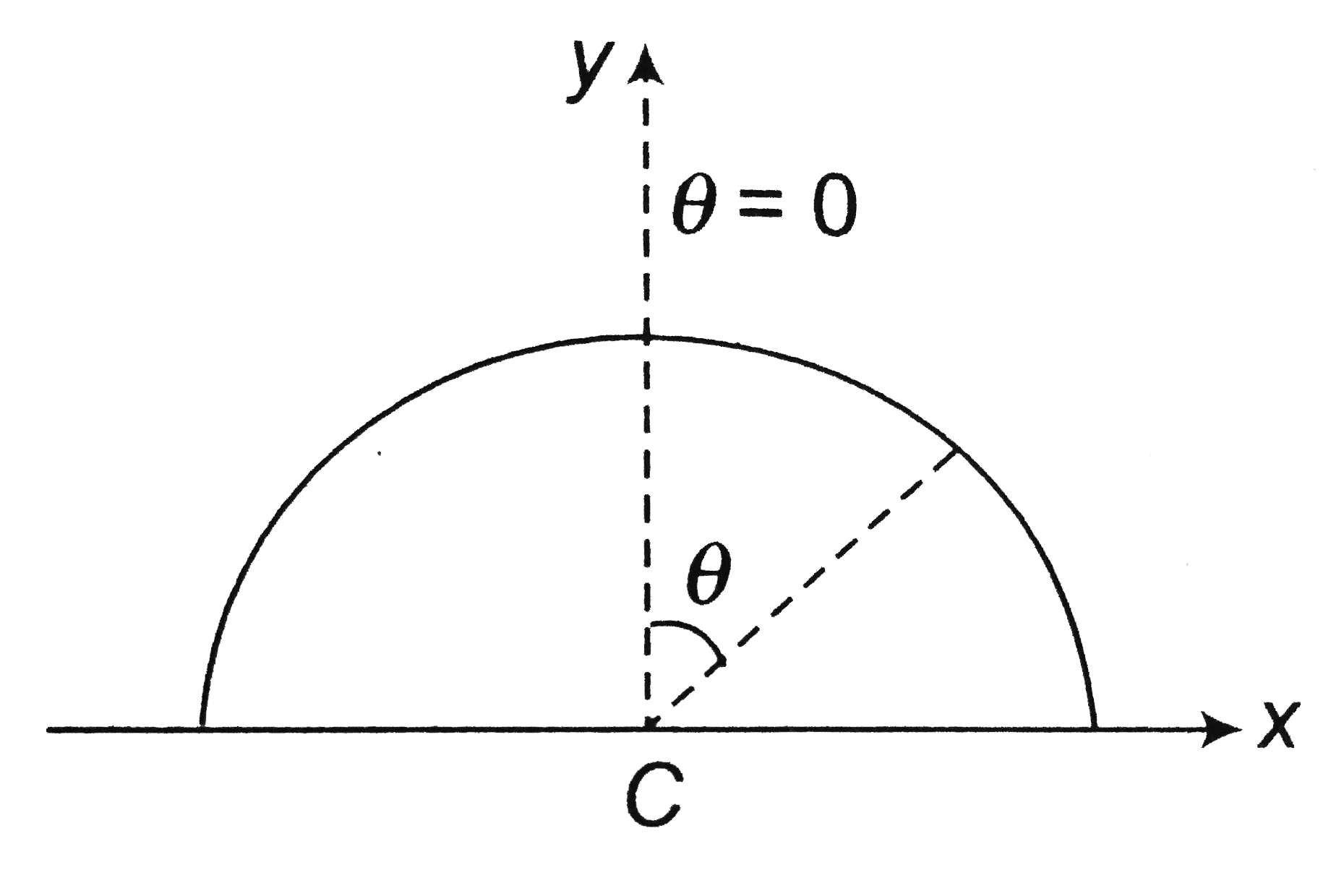
View SolutionA semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
View Solution
