Find the area of region by the curve $y = sin x between x = 0 and x = 2 π$ .

A

5 sq units

B

$4$ sq units

C

$3$ sq units

D

$7$ sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Required area $= \int_{0}^{2 π} sin x d x = \int_{0}^{π} sin x s x + ∣ ∣ ∣ \int_{π}^{2 π} sin x d x ∣ ∣ ∣$
$- {[cos c]}_{0}^{π} + ∣ ∣ {[- cos x]}_{π}^{2 π} ∣ ∣$
$= - [cos π - cos 0] + | - [cos 2 π - cos π] |$

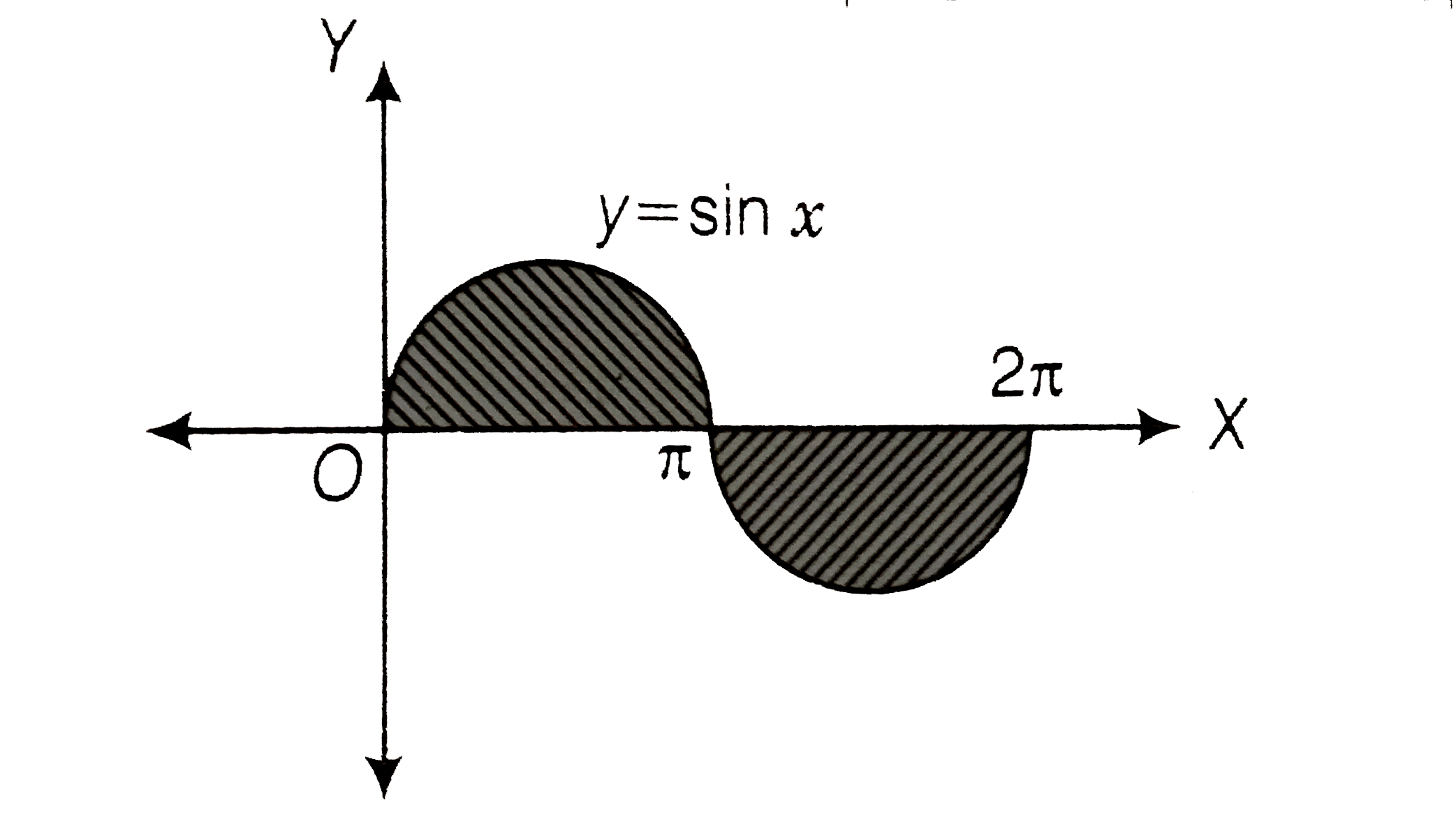
$= - [- 1 - 1] + A B S (- (1 + 1))$
$= 2 + 2 = 4 sq units$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the area bounded by the curve y =sin x between x=0 and $x = 2 π$ .
A1 sq unit
B2 sq units
C3 sq units
D4 sq units
What is the area of the portion of the curve $y = sin x,$ lying between x=0,y=0 and $x = 2 π$ ?
A1 sq. unit
B2 sq. units
C4 sq. units
D8 sq. units

NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals

Home
Ask Doubt
Profile