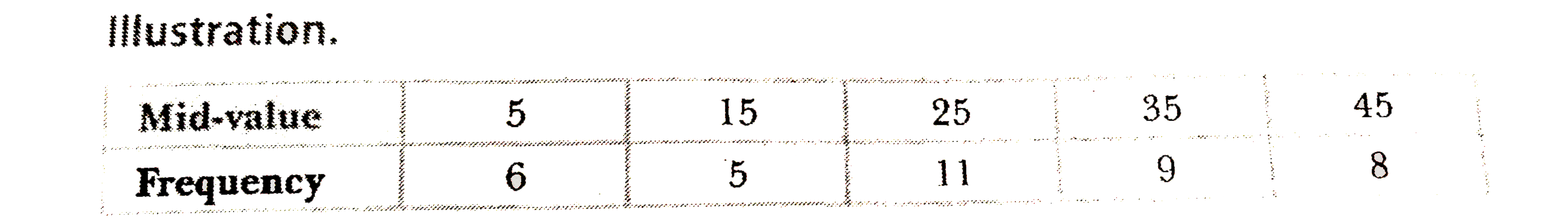
Such series may be converted into simple frequency series using the following method:
(i) First, mutual difference between mid-values (i), is determined, and (ii) Second, the difference so obtained is reduced to half (12i) which when deducted from the mid-value gives lower limit of the class interval and when added to the mid-value gives the corresponding upper limit.
Thus, Lower limit: l1=m−12i
Upper limit: l2=m+12i
where, m=mid-value, i=difference between mid-values, l1=lower limit and l2 = upper limit.
In the above frequency series with mid values, the mutual difference between mid-values (i) 15 - 5=10. Half of it is 5. Deducting 5 from each mid-value we get lower limits and adding 5 to each mid-value we get the corresponding upper limits.
Following table shows the process of this conversion.

Topper's Solved these Questions
- ORGANISATION OF DATABOOK - TARUN JAIN & VK OHRICHAPTER - ORGANISATION OF DATAEXERCISE - Miscellaneous Illustration
13 Videos
- ORGANISATION OF DATABOOK - TARUN JAIN & VK OHRICHAPTER - ORGANISATION OF DATAEXERCISE - EXERCISE M.C.Q
10 Videos
- MEASURES OF DISPERSIONBOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF DISPERSIONEXERCISE - Learning by doing
30 Videos
- PRESENTATION OF DATA - TEXTUAL AND TABULAR PRESENTATIONBOOK - TARUN JAIN & VK OHRICHAPTER - PRESENTATION OF DATA - TEXTUAL AND TABULAR PRESENTATIONEXERCISE - ESSENTIAL PRATICALS
8 Videos
Similar Questions
In ______ , lower limit of the first class interval and the upper limit of the last class is not given . (open end series / mid - value series)
View SolutionThe following tables gives the current i (in amperes) through two devices for several values of potential difference V (in volts). From these data, determine which device does not obey Ohm's law.

View Solution
Knowledge Check
Evaluating integrals dependent on a parameter:
Differentiate I with respect to the parameter within the sign an integrals taking variable of the integrand as constant. Now evaluate the integral so obtained as a function of the parameter then integrate then result of get I. Constant of integration can be computed by giving some arbitrary values to the parameter and the corresponding value of I.
The value of dIda when I=∫π/20log(1+asinx1−asinx)dxsinx (where |a|<1) isAπ√1−a2B−π√1−a2C√1−a2D√1−a2πStudy the following information and answer the questions that follow.
A number series is given as 20, a, b, c, d, 65
Where a, b, c and d are missing terms.
It is also given that:
I. a – 20 = (x2 + y)
II. The value of b is greater than a and the difference of b and a is equal to the
[(x+1)2+y]
III. The value of c is [(x+2)2+y] more than b and the value of d is [(x+3)2+y] more than c.
Note: x is equal to the HCF of 2 prime numbers and the value of y is equal to the smaller root of the quadratic equation z2–z–6=0.
If another series follows the same pattern as the given series and the first term of this new series is 29, then find the fifth term of this new series.A67B56C42D51Study the following information and answer the questions that follow.
A number series is given as 20, a, b, c, d, 65
Where a, b, c and d are missing terms.
It is also given that:
I. a – 20 = (x2 + y)
II. The value of b is greater than a and the difference of b and a is equal to the
[(x+1)2+y]
III. The value of c is [(x+2)2+y] more than b and the value of d is [(x+3)2+y] more than c.
Note: x is equal to the HCF of 2 prime numbers and the value of y is equal to the smaller root of the quadratic equation z2–z–6=0.
Which of the following is/are divisible by (y + 5)?AA. Only dBB. Only a and bCC. Only b and dDD. Only a, b and d
(a) During roasting most of the metals are converted into their respective oxides which are then reduced to the corresponding metals by using suitable reducing agents. However, it has been seen that in some cases, instead of the metal oxide, it is the metal which is isolated.
Read the above passage and answer the following questions :
(i) Name two metal sulphides which are converted into the corresponding metals during roasting. When does it happen so ?
(ii) Name two metal sulphides which get converted into the corresponding metals during roasting. When does it happen so ?
(b) What is a flux ? What is the role of a flux in teh metallurgy of iron and copper ?
(c ) How is wrought iron different from steel ?
View SolutionThe following table given the values of refractive indices of a few media.
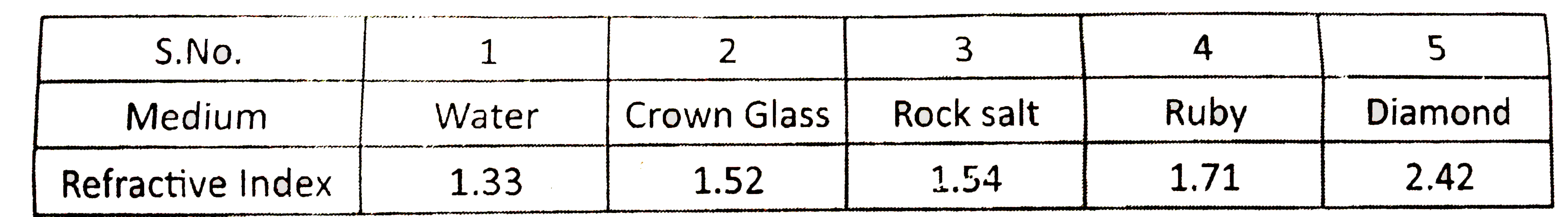
Use this table to give an example of (i) a medium pair so that light speeds up when it goes from one of these media to another (ii) a medium pair so that light slows down when it goes from one of these media to another.
View SolutionA sinusoidally alternating emf is applied to an LCR series circuit . (i) Define the impedance of the circuit . (ii) Obtain the expressions for the impedance and the phase difference between the emf and current from the phasor diagram. (iii) Discuss the behaviour of the circuit for different relative values of the two reactances in the circuit.
View SolutionIn case of inclusive classes the first step is to convert the same into exclusive classes by using adjustment value to change the limits ( See section 4.3.3.). Given the following frequency distribution with inclusive classes.

The adjustment value for converting inclusive classes into exclusive classes is 0.5(=6−52). Deduct 0.5 from all the lower limits and add 0.5 to all upper limits before applying the method of calculation.
View SolutionStudy the following information and answer the questions that follow.
A number series is given as 20, a, b, c, d, 65
Where a, b, c and d are missing terms.
It is also given that:
I. a – 20 = (x2 + y)
II. The value of b is greater than a and the difference of b and a is equal to the
[(x+1)2+y]
III. The value of c is [(x+2)2+y] more than b and the value of d is [(x+3)2+y] more than c.
Note: x is equal to the HCF of 2 prime numbers and the value of y is equal to the smaller root of the quadratic equation z2–z–6=0.
What is the value of d?
View Solution
