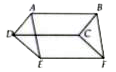
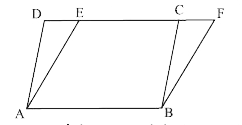
In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
Video Solution
Text Solution
Given: ABCD and AEFD are two parallelograms.
To prove : ar(ΔPEA)=ar(ΔQFD)
Consturction : Join PD.
Proof: In ΔPEAandΔQFD,
∵⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩∠APE=∠DQF(∵ corresponding angles are equal as AB∣∣CD)∠AEP=∠DFQ(∵corresponding angles are equal as AE∣∣DF) AE=DF(∵ opposite sides of a parallelogram are equal)
∴ΔPEA≅ΔQFD (by AAS congruence rule)
Hence, ar(ΔPEA)=ar(ΔQFD) ( ∵ congruent triangles have equal aras)
|
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD and AEFD a re two parallelograms.
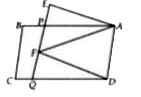
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.

PE =ABPBFQCAPDCQIn the given figure, ABCD and AEFD a re two parallelograms.
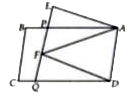
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
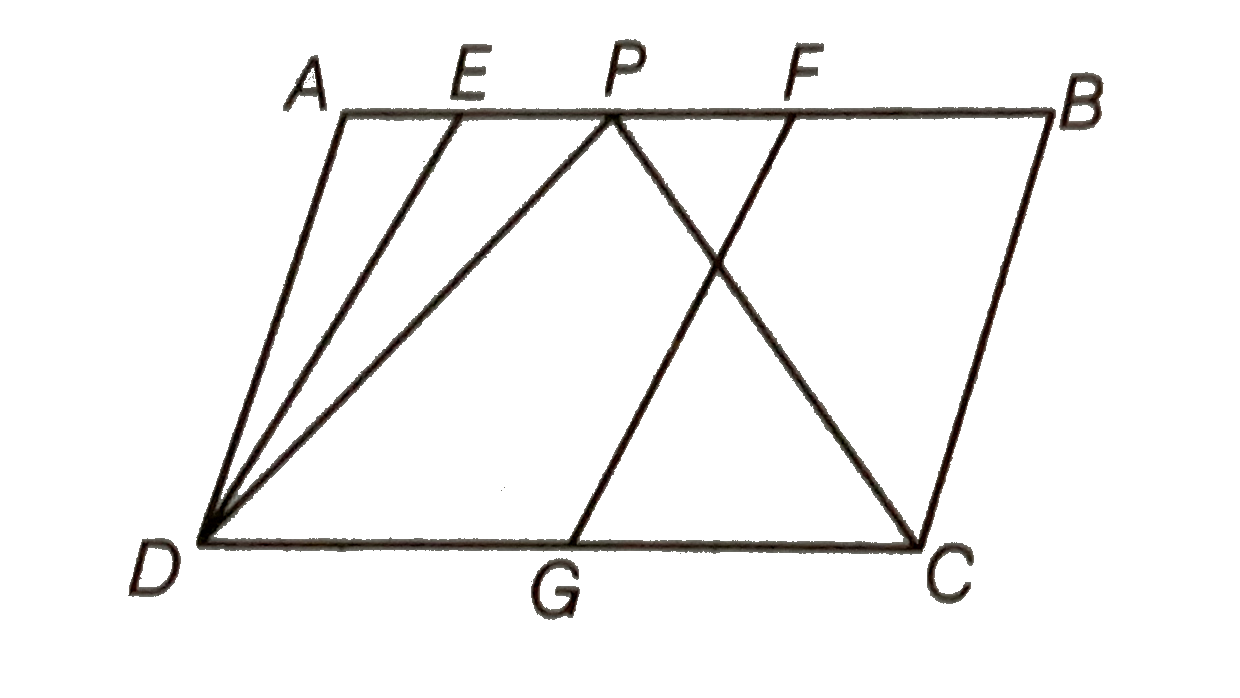
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
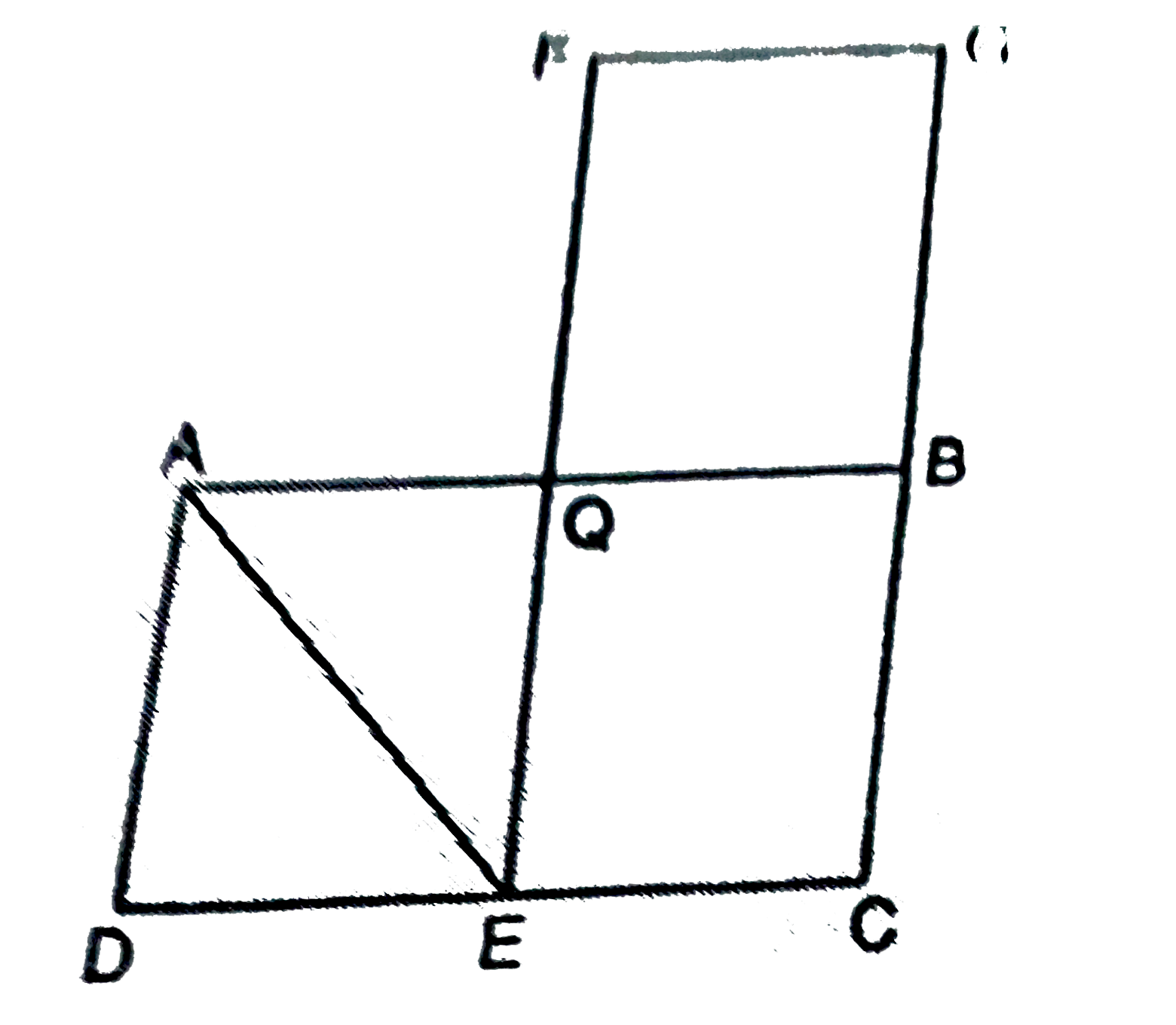
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View SolutionIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
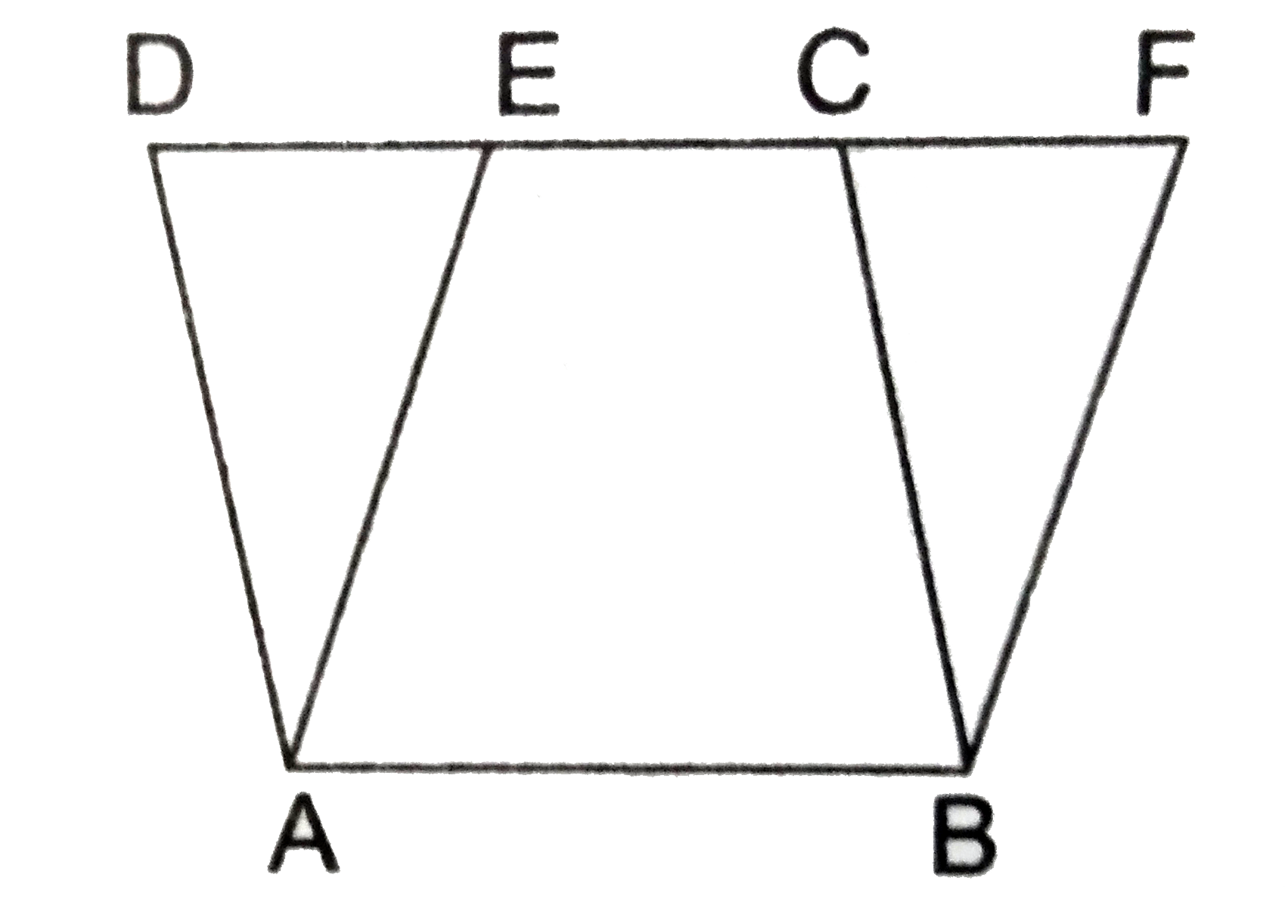
View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
View Solution